mech2 102

202

Zadania 2 (rys. 1.53)

Pręt o długości 21 i masie M obraca się z prędkością kątowi wokół nieruchomej osi, która przechodzi przez koniec 0 pręta i tw'. z nim kąt a . Wyznaczyć kręt względem punktu 0.

Odp. K° = K_y = | M l² ułsin a„

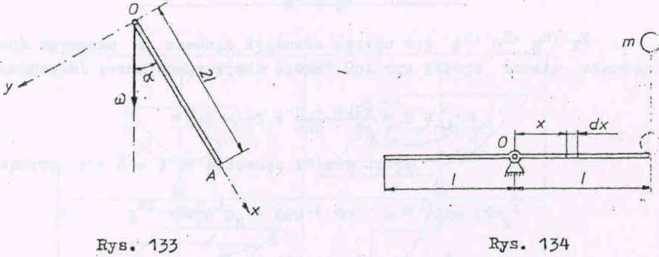
Zadanie 5 (rys. 13*0

Belka o długości 21 i masie M może obracać się swobodnie w: osi poziomej, przechodzącej przez jej środek ciężkości. Początkowo b;. zajmowała położenie poziome i pozostawała w spoczynku do chwili, gdy jej koniec spadł pionowo z wysokości h kawałek wilgotnej gliny o sie m i przylgnął. Wyznaczyć prędkość kątową belki po uderzeniu.

Rozwiązanie

W krótkim okresie dt, zawartym między ohwilamii tuż przed ude? niem i tuż po uderzeniu, kręt układu złożonego z belki i kawałka g.i. względem osi obrotu belki nie ulegnie zmianie. Kręt przed uderzeniem,

K₁ = m v_pl = o 1 yigh ,

gdyż prędkość belki równa jest zeru, a gliny v_p = lf2gh. Kręt po u rżeniu:

K₂ = I u> + m v 1.

Moment bezwładności belki (pręta) o długości 21 względem jej osi ob

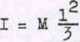
Prędkość masy m przy obrocie belki

v =

203

K₂ = Mij-io+ml²tu= ul²

.!*■>

ównująo kręty otrzymamy:

m l/2gh l=a) l^j + m^ ,

_ 5m V2gh “ “ UM + >J •

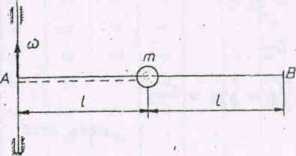
Zadanie 4 (rys. 135)

Gładkie poziome ramię AB, o długości 21 i masie U Jest w końou A zymocowane do poziomej osi z, a w końcu B me małą nasadę. Na ramieniu że swobodnie przesuwać się ciężarek o masie m (ale nasada nie pozwo-mu zejść z ramienia). Początkowo ciężarek jest przywiązany do osi ni-ą o długośoi 1 i wszystko obraoa Bię z prędkośoia kątową u p. Jaką ędkość kątową będzie miał układ, gdy nić zerwie Bię i ciężarek dojdzie B.

4M + 3m oj —...    —,

Odp.

ui =

o 4 (id +3 raj

\

Z\

Rys. 135

Zadanie 5

Swobodny sześolan wiruje z prędkością kątową w wokół przekątnej, trzymujemy jedna z krawędzi nie przecinających owej przekątnej, Wyzna-yć nową prędkość kątową.

' Odp.

u =

u).

4 YJ ^w

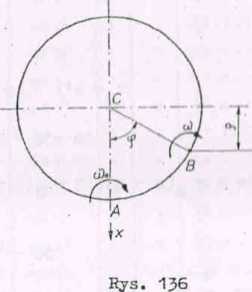
Zadanie 6 (rys. 136)

Okrągła tarcza obraca się z prędkością kątową to wokół punktu A ojego obwodu. Wyswobadzamy punkt A i jednocześnie⁰ zatrzymujemy inny nkt 3 obwodu. Kąt ACB = ®, przy czym C oznacza środek tarczy. Wyzna-yć prędkość kątową tarczy podczas obrotu dookoła punktu B. Gdzie powi-en leżeć punkt B, aby tarcza zatrzymała się?