049

49

2.4. Funkcje charakterystyczne

Rozwiązanie.

Funkcja charakterystyczna zmiennej losowej X wyraża się wzorem

		0 1
	9(0 = j e^,txf(x)dx —	/ e"'^c(l +x)dx+ 1 e"*(l	— x)dx.
		•/ J -1 0
Ponieważ	1 xc^itxdx = jt [xc^ltx ~	■^e"^jcj oraz j e"^A dx	= -e^Uxit
więc	9(0 = \	\ it it it)

Korzystając ze wzorów

e“ = cosr + /sinr,    e~“ = cost — isinr,

otrzymujemy

9(0 =

W^(cos'~ⁿ'

Ponieważ 1 — cos t = sin² 5, więc

9(0 =

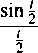
2

Zadania

Zadanie 2.4.1.

Niech X i Y będą niezależnymi zmiennymi losowymi o rozkładach normalnych Nim,, c,) i N(m₂,<T₂). Znaleźć rozkład zmiennej losowej Z = X — Y.

Zadanie 2.4.2.

Obliczyć funkcję charakterystyczną zmiennej losowej X, dla której Pr(X = kn/n) = 1 /n dla k = 1,2,... ,n.

Zadanie 2.4.3.

Niech X ma rozkład geometryczny, tzn. Pr (Z — k)= q^k~^] p, k= 1,2,.... Obliczyć jego funkcję charakterystyczną i korzystając z niej wyznaczyć F.X i D²X.