054

54

Rozkład t-Studenta

Rozkład Sne de córa

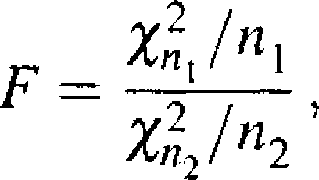
2. Zmienne losowe

czyli kwantyle £,_x__a = %a dla danego a i danego n < 30. Takie tablice są też zamieszczone w tym skrypcie.

Rozkładem związanym z rozkładem chi-kwadrat Pearsona jest rozkład r-Studenta określony jako rozkład zmiennej losowej t danej wzorem

X

t — t_n — _r ,    (2.4.13)

\fx[/n

gdzie X ~ N (0,1), a x» ma rozkład chi-kwadrat o n stopniach swobody oraz X i ^s4 niezależne. Rozkład r-Studenta jest również asymptotycznie normalny N(0,1), przy czym podobnie jak dla rozkładu chi-kwadrat, przybliżenie jest dobre już dla n > 30. Liczbę n tak jak dla rozkładu chi-kwadrat, nazywa się liczbą stopni swobody. Rozkład f-Studenta jest symetryczny, Et = 0 dla dowolnej liczby stopni swobody oraz D²t — n/(n — 2) dla n > 2. W tablicach podaje się zwykle liczby t_a, dla których zachodzi równość

Pr(f >*«) = <*,    (2.4.14)

czyli kwantyle Ę_)]„_a = t_a lub też wartości

Pr(|/| > t_a) = a,    (2.4.15)

dla danego a i danego n ^ 30. W skrypcie umieszczone są tablice zarówno wartości dystrybuanty rozkładu /-Studenta, jak i wartości t_a dane wzorem (2,4.15).

Następnym rozkładem związanym z rozkładem chi-kwadrat Pearsona jest rozkład Snedecora określony jako rozkład zmiennej losowej F danej wzorem

(2.4.16)

gdzie    i Zn., ^s4 niezależnymi zmiennymi losowymi o rozkładach chi-kwadrat

0    n_x i n₂ stopniach swobody. Mówimy, że zmienna losowa F określona wzorem (2.4.16) ma rozkład Snedecora o (w₁,n₂) stopniach swobody.

Podobnie jak dla rozkładu chi-kwadrat, podaje się wartości F_a dla których Pr(F > F_a) = a dla danego a (wartości krytyczne). W tablicach na stronach 124-126 podane są wartości F_a dla a = 0.05 i stopni swobody n_{ — 1,... ,30

1    n₀ — 1,...,30.

Jeżeli zmienna losowa F ma rozkład Snedecora o (n_x,n₂) stopniach swobody, to ze wzoru (2.4.16) wynika, że 1 jF ma również rozkład Snedecora, ale o («₂,rt|) stopniach swobody. Dlatego do wyznaczenia F,__a dla (n_vn₂) stopni swobody wystarcza znajomość F_a dla (n₂?n_x) stopni swobody. Niech Pr(F >