075

4.1. Definicje

Ib

Twierdzenie 4.1.7.

Niech X, ,X_n,... ,X_rt , Y,, F₂,..., Y_n będą próbami prostymi z dwóch niezależr

1    ^    J    *    4

nych populacji o skończonych wariancjach. Wdwczay statystyki

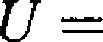
X — Y — (m_[ — m₂)

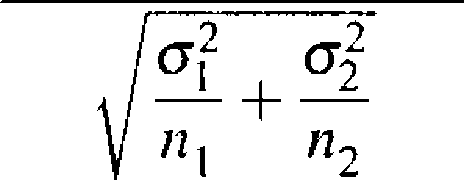
oraz

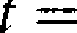
X — Y — (m_] —

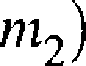
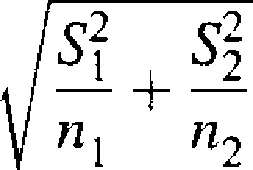
(4.1.12)

są asymptotycznie normalne N(0,1) dla n_{ —°o i n₂ —» ⁰⁰.

Twierdzenie 4.1.8.

Mcc/i X_Ł ,X₂j... ,X„ , T_Ł ,T₂j • ■ • >    Pfóbami prostymi z dwóch niezależ

nych populacji o rozkładach normalnych, odpowiednio N(m,, <jj) i N(m₂,o~>). Wówczas statystyka

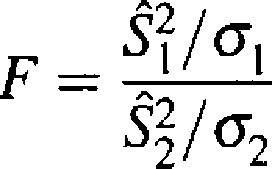
(4.1.13)

ma rozkład Snedecora o (/ij — l,n₂ — 1) stopniach swobody.

4.1.4. Zadania

4.1.1.    Dokonano 20 niezależnych prób, otrzymując następujące wyniki:

0.50, 0.93, 0.75,    0.89, 0.15,    0.94, 0.16,    0.00, 0.63,    0.57,

0.33, 0.10, 0.14,    0.21, 0.05,    0.15, 0.37,    0.51, 0.09,    0.25.

Obliczyć X, S² i S². Dane liczbowe do tego zadania znajdują się w pliku dane20.dat.

4.1.2.    Dokonano 30 niezależnych prób, otrzymując następujące wyniki:

1.05, 1.13, 0.41,    0.12, 0.12,    0.19, 3.02,    0.08, 3.87,    0.54,

2.63, 0.40, 1.15,    0.24, 0.46,    1.07, 0.58,    0.29, 0.56,    2.11,

0.40, 0.04, 0.74, 1.41, 0.18, 3.14, 0.40, 0.64 0.29, 2.47.

Obliczyć X, S² i Ś². Dane liczbowe do tego zadania znajdują się w pliku dane30.dat.

4.1.3.    Przeprowadzić następujący eksperyment: rzucić 50 razy monetą, a następnie obliczyć zaobserwowane wartości statystyk X, S² i Ś², gdzie X jest liczbą reszek w 50 rzutach. Porównać x, s² i s² z EX, D²X.