124

124

Odpowiedzi i wskazówki

2.3.25. Dystrybuanta

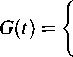
(O    dla i < O,

\l-e-*"' dla t ^ 0.

Gęstość

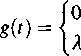
j 0    dla t < 0,

\xne^^lnt dla t ^ 0.

Zatem T ma rozkład wykładniczy z parametrem nX.

2.3.26.

2.3.27.    p_n = 1 — (1 — 1 /n)ⁿ. Stąd lim p_n = 1 — e *.

n—»oo

2.3.28.    Pr(x² < 18.15) w 0.8. Ponieważ Pr(^² > 26.8728) = 0.02 i Pr(%² > 29.1412) = 0.01, więc poprzez interpolację liniową Pr(%² > 28.10) = 0.0146. Zatem Pr(^² < 28.10) =0.9854.

2.3.29.

a)    Szukamy Xa takiego, aby Pr(x² < Xa) = 0.60. Bezpośrednio z tablic odczytujemy X²a = 15.7332 dla a = 0.40, stąd Pr(^² ^ 15.7332) = 0.60, czyli kwantyl ₆₀ = 15.7332.

b)    Ponieważ Pr(%² > 15.7332) = 0.4 i Pr(x² > 14.3389) = 0.5, więc poprzez interpolację liniową otrzymujemy Pr(z² 15.3149) = 0.57. Zatem kwantyl Ę,₀₅₇ = 15.3149.

2.3.30. Pr(f„ > 0.73) = 0.5Pr(|f„| > 0.73). Z tablic odczytujemy wartości sąsiednie liczby 0.73 dla danego n. Gdy n = 4 są to Pr(|f₄| > 0.5686) = 0.6 i Pr(|f₄| > 0.7404) = 0.5. Rozwiązanie otrzymujemy przez interpolację liniową.

n	4	9	12
Pr(r„ > 0.73)	0.2531	0.2424	0.2403

2.3.31. Wskazówka. Rozwinąć gęstość tego rozkładu w szereg Maclaurina, scałko-wać wyraz po wyrazie, a następnie obliczać sumy częściowe tego szeregu, aż moduł

reszty będzie mniejszy od zadanej dokładności. Ponieważ e“ =    , więc e^-^² =

^^_1)*2*it! °^{raZ dlax}^^0: