17 (5)

Biblioteczka Opracowań Matematycznych

Warto wymienić następujące:

a/jeżeli funkcja podcałkowa zawiera pierwiastki np.: jR(x,yJax+b)dx to aby wyznaczyć całkę należy zastosować podstawienie: ax+b=t".

b/jeżeli funkcja podcałkowa zawiera pierwiastek kwadratowy z trójmianu kwadratowego typu:

(1-29)

to dla wyznaczenia całki należy zastosować pierwsze

podstawienie Eulera. Pomijając szczegóły wyprowadzenia wzoru otrzymu-

-jemy:

(1.30)

W ten sposób obliczamy każdą całkę postaci

gdzie a>0.

dx

c/ każdą całkę postaci całkę:

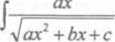
gdzie a < 0 obliczamy wykorzystując

(1.31)

d! całki postaci    +bx + cdx gdzie a < 0 wyznaczamy wykorzystując wzór:

(1-32)

e/ całki postaci

obliczamy korzystając ze wzoru:

(1-33)

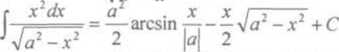
f/ całki postaci (1.34)

gdzie a > 0 wyznaczamy ze wzoru:

f x¹dx

g/ całki postaci Jlf^TbxTc £^^z*^{e a >} 0, wyznaczamy ze wzoru:

(1.

•35) f    = -Wjt² + k--Łln|jf + Vx² + k

2    2 I

+ C

. J-

h/ przy obliczaniu całek postaci dax¹+bx+c stosujemy metodę współczynników nieoznaczonych. Metoda ta zostanie przedstawiona na przykładach.

PRZYKŁADY CAŁKOWANIA

105/

^JV4x + l

4jc + 1 =/^j 4dx = 2 tdt

r²-i

= f—2-‘-dt = i f/^J + \dt = —+/ + C =

^J /    2 4^J    12

_ V(⁴-* + O’

12

+ V4jr+1 +C

V* + >/x

f6>V)    <• 6/⁵a!r _ rrV/

•* /² + r³ 3 r² (l -t- /) M + /

106/ j

x = r

dx - 6l'dt

Kfx = /^j,V7= /

=6^-r+1 ~ J*=^-t^-61ij/+C=^+3^-61ij^+l|+C

-33-