14 (7)

Biblioteczka Opracowań Matematycznych

-2h.|x-2|-J^ + C

4x³ - 4x +1    ■* 4x² — Az +1 X J Ar¹ -

4x — 4x +1

l r_

1 Jlr² -4i

1 r dx

8 ¹    ' 2 J(2x-l)² ” 8 ¹    ' 2

1 _r di I

- -lnUjt² - 4x +1| — \-o I    I 9 U

8 ³ 4x² - 4x +1    2 ^J 4x² - 4x +1

2x -1 = /

2 dx - dt

= -Ink*² - Ax +1| - —

-- r^-=Iin|4x³-4x + l|- -_r^-r + C

4V 8 ^{1    1} 4(2x-l)

r2x²-5x + l ,    ,

92/ J ₃ . ,-dx = l

’ x - 2x + x

= —In|4x^J-4x+l| 8 ¹ 1

2x² - Sx+1 _ 2x²-5x+l _2x^;-5x+l    .4 B C x²{A+B)+x{C-B-2A)+A

x³-2x*+x x(x^J-2x+l) x{x-l)*’ x⁺x-l ⁺ (x-l)²    x(x-])²

A + B = 2 C- B-2A = -5 A = 1

I

93/

5x-l

^4 = 1 B = 1

C =-2

dx

x-I

-+C

J._.5_£Z.L_^₌ f _i

V-3x-2    ^Jx³-2x-x-2

5x —1    5x-l

ABC -+ ----

(x’ -x)-2(x + l) x(x^! -l)-2(x+l) (x + l)^:(x-2) x + 1 ⁺ (x+ l)^{2 +} x-2

x^:(A + C)+x(-A+B+2C)+(-2A-2B + C)

(x+l)-’(x-2)

A + C = 0	/J = -l
-A+B+2C=5	B = 2
-2B-2A + C = -l	C = 1
r * , r	dx	-ln|x + l|--— + ^1 M X+1
^Jx + I ' ‘■^J(x + 1)^2 Jx-2

Biblioteczka Opracowań Matematycznych

94/

f ⁵*+²    a

3 V²    3 y

’x +2x+10

-(2x + 2)-3

x² + 2x + 10

<Lx = -\ ■) 3

5 r 2x + 2 2 Jjt^I+2jr + 10

dx-3}

dx

jc¹ + 2jc + 10

= — InLr² + 2x + 10|-3 f.- ■ ^-= -ln|x² -2x + l0|-arc/g^:^^- + C

2 ^{1    1 J}(x + l)²+9    2 ^1    1    3

( Wykorzystano wzór (1.26)).

Jx³-2x^:

x + 2	x+2		ABC
x^3 -2x^2	“*^2(	x-2) '	' 7 ' x x x-2
A+C = 0		/4 = —1
5-2/4 = 1		5 = -1
-25 = 2		C = 1
f-«fr	, f	-<fr	r c& 1
^/_J *	' J	x^2 '	' 2x - 2 ’ x
96/	v- ^Jx-2 ^J x-2

97/

k^A

X^>

²(x-2)

dx

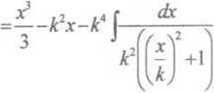
=--k*x-karctg\ — +C

C 2x²+x + 4 j _ (•    2x² +x+ 4    _ r 2x²+x + 4    _

2§/    Jx³+x²+4x + 4    ^x²(x+l)+4(x + l)    ^(x² + 4)(x+lJ

2x² + x + 4    A    Bx+C x²(A +    B)+ x(B + C)+ 4A    +C

(x² + 4)(x + l) x + I x² + 4    (x² + 4)(x + l)

A + B = 2    (A = l

B + C = \ |s = l    / =    f _^_+    f_f^_=    |_n|x + l| + —ln|x²+4I    + C

4,< + C = 4 [c = 0    ^J * + I x+4    2