2011 12 19#;01;263

\G(ju>)\ = ——^z=r- = —p===-

tykft+Pf (yw»+l f

Zapas fazy Uczymy dla modułu równego 1, więc: - = ^l ->    (Vu2+1)³ = 4

(/wł+iy*

(w* + l)³ = 10

- to Jest u dla której moduł wynosi 1.

A<f> = 180° — 3arctan(ui) = 27.1°

Zapas wzmocnienia

AA = — = - = 2 Ml 2

bl Korektor szeregowy

Korektor szeregowy ma ogólną postać:

- wyznaczanie A

7W1

TT*+*

Transmitancja układu z korektorem;

6»= ^{4 <7}’^lJ,+l

4i4Tta + 4/4

*l + 3»-’ + 3a + I Uchyb układu z korektorem:

-y . UM £,(«) =

5-+i

(aJ+3at+3a+l)(^a+l)

l+CuJa) ,_ł_JJ7WU

(.i+J»z+l«+l)<™*+l)

_ ,    (a* + 3«ł+3e + l)(£e + l)

* (*l+3*z + 3e + l)(£. + l)+4,47\e+4i4

Uchyb ustalony układu z korektorem:

,    (»>+3.s+3a + l)(^a + l)

tJ„(a)= HmaK(s)= lima;-

M “♦ 0    *-*0 ¹

(*>+3e*+3j+l)(^a+l)+4/4TŁe+4i4

I

4/4 + 1

Jeśli uchyb ustalony ma być równy 0.05, to: ₌    A-19/4.

- wyznaczanie a

a =

A

±

19

- wy*^nacz*nlc Te

° ljuf+3(juf+3ju+l [1 lm[G{ju)\ = 0    “>    3<*»—w^J = w{3-(J^ł) = 0

czyli to co not Interesuje to: w=*JŚ

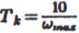
JO

Ostatecznie korektor ma postać:

12 J^L

4 ' t lO

Ja_J+1

»+i

Na dziennych dawał Jeszcze przeregulowanie I czas ustalenia, ale nam raczej nie da - za dużo liczenia ł chyba nawet nie robił przykładów.

3