23 (5)

Biblioteczka Opracowań Matematycznych

Pomocniczo rozkładamy funkcję wymierną na ułamki proste: t+\    1    2

/(/-l) t ⁺1-1

/= \~~~⁺ 2    ⁼ — ln|f| + 21n|f —l| + C = - In e^x + In(e* - l)² + C

fdt

142/

_re^3x<ir

e^2x    i i

=--2e* + 41n|e^x + 2| + C

143/

r    dl r dl r dl    cdi l r dl \ c dl

V^x-<?^x    I *    /    V(/^J-l)    ■'/²(/²-l) Jr² + 2-l/-l    2-I/ + 1^-

=7+}^,nk->l-}>ⁿk+^,l=jr+^^lnh^,-¹|-}^lnk⁺¹l^+c

Pomocniczo rozłożono funkcję wymierną na ułamki proste:

1_ A    B_ C_ D ₌    1    I__1_

f²(/² - i) / ⁺ r^{2 +}r-I⁺r+l " r²⁺2(/-l) 2(/ + l)

144/    i

1 _

f

■e —e

e*+e-^x

,    ,    , dl

-dx= e -t dx= —

^J/+l /    +1 / ^JV / t +\J    ^J/²+l

i

= -ln|e^x| + ln|e^2x + l| + C = In|e^2x + l|-x + C 145/    ¹    1

f 3 -r .	« = x^3	du = 3x^2dx	_I*- « f 1 -r*	u = x^2	du = 2xdx
Jx e dx =	dv = e~^sdx	v = -e‘^x	= -xe + 3jx^2e dx	* M II ■s	v = -e~‘

u = x du = dx dv = e^x v = -e'

= -xe~* -3x²e * + 6 jxe~*dx =-x³e ¹ -3xV' +6 = -x³e~^x - 3xV^x - 6xe'^x + 6 je~*dx = -xe'^x - 3x V^x - 6xe‘^x - 6e'^x + C

146/a‘dx 'a^łI + 1 "

a* = / Ina* = ln/ dx =

dl

/Ina

<• dl    1 r dt

•1 In a(r +1)    lna-'/^?+l

= —arctgt + C = —— arctg(a^I)+ C Ina    Ina

147/

flo£,x4r = f^{ln X}^^V = —fln xdx = —J— ^{J 65 J} In3 ln3^J    In3

dx

u = In x du =

x = x

dv = dx

Do wyznaczenia całki 147/ wykorzystano wzór: 3^{1 2 3}*^,x = x In 3 log ₃ x = In x log ₃ x = *ⁿ X

148/

e”dx

V 1 + e ³¹ =/ -

2e^3xdx

= dl

ln 3

(x In x-x)+C

(1.43)

+ e

In 3

3¹    3    3

(1.44) sinh x = shx =

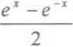
(1.45)

cosh x = chx =

2

(1.46)    sinhx e‘-e~‘

tgh* -—7—=—--

cosh x e - e

(1.47)

ctghx =

cosh x sinh x

e +e

e -e

(1.48) _cosh ² x = 1 + sinh² x

(1.50) _lt2_x ch2x +1

^{C A_} 2

(1.52)    sh2x

shxchx = -

2

(1 -54) J_c/ixo!v = shx + C

(1.49) cosh 2x = cosh² x + sinh² x

0-51)

9

(1-53) |shxdx = c/ix + C

<¹⁵⁵> \^ = 'kx + C ' ch¹x

-45-

1

Całki funkcji hiperbołicznych_

2

Całki funkcji hiperbołicznych wyznacza się tymi samymi sposobami

3

co inne całki. Należy wykorzystywać wzory dotyczące związków pomiędzy tymi funkcjami oraz wzory- dotyczące całkowania funkcji hiperbołicznych. Poniżej podane są najważniejsze z nich.