matrozw6

190 2. ROZWIĄZANIA I WSKAZÓWKI

8. Obszar D jest wDętrzem prostokąta. Ponieważ

190 2. ROZWIĄZANIA I WSKAZÓWKI

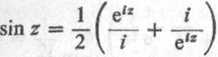
więc odwzorowanie (1.5.25) jest złożeniem czterech odwzorowań: obrotu    = iz

odwzorowania w₂ = e^wi obrotu    w₃ = — iw ₂

odwzorowania Żukowskiego w = — [ w₃ + -J—

2 V ^W3

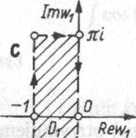
Obrót w₂ = iz przekształca obszar D na obszar D_u który jest także wnętrzem prostokąta (patrz rys. 2.5.2). Odwzorowanie

w₂ — e^Wl czyli w₂ — e^Rewi e^,ImWł

-Ki

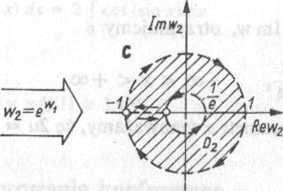
Rys. 2.5.2 przekształca obszar D₁ na obszar D₂, którego brzeg składa się z dwóch okręgów:

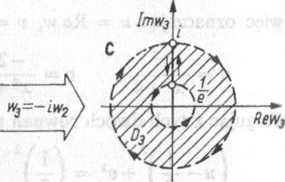
k₂| = — i lw₂| = 1 oraz odcinka o końcach — — oraz -1. Obrót w>₃ = -iV₂ od-e    e

wzorowuje obszar D₂ na obszar D₃, którego brzeg składa się z tych samych co poprzednio okręgów i odcinka o końcach — i oraz L Wyznaczymy obraz okręgu |w₃| =

e

= — w odwzorowaniu Żukowskiego. Ponieważ równanie tego okręgu można zapi

n>₃ = — (cos (p+1 sin (p), e

sać w postaci 1

(patrz rys. 2.5.2), więc jego obraz ma równanie

w

= y [(^e+ y)cos<p-/^e- yj sinpj, -y* <? < y

Oznaczając u = Re w oraz v — Im w otrzymujemy stąd równania parametryczne obrazu okręgu |w₃| = 1 w odwzorowaniu Żukowskiego

{u = ch 1 cos (p    3    rt

...    - -sr« <(P<Ty

v = — sh 1 sin cp    2    2

Równania te przedstawiają elipsę o półosi dużej ch 1 oraz półosi małej sh 1. Równaniem osiowym tej elipsy jest

sh²l*w² + ch²l-t;² = cb²l sh²l    (2.5.1)

Obrazem okręgu |w₃| = lw odwzorowaniu Żukowskiego jest odcinek o końcach — 1

i 1, natomiast obrazem odcinka o końcach — i oraz i jest odcinek o równaniu

e

w

(2.5.2)

czyli odcinek o końcach —sh 1 i 0. Ostatecznie, odwzorowanie (1.5.25) przekształca obszar D na obszar Q ograniczony elipsą (2.5.1), odcinkiem (2.5.2) oraz odcinkiem o końcach —1 oraz 1. Na rysunku 2.5.2 ilustrowano to odwzorowanie. Obrazem

punktu y i jest punkt — i sh --.

9. Obszar D jest podzbiorem obszaru P, którego odwzorowanie za pomocą funkcji (1.5.26) było badane w zad. 3 (patrz rys. 1.5.13). Obrazem odcinka o końcach — oraz — w odwzorowaniu (1.5.26) jest odcinek o równaniu w = cos*, < 4    2    /2    ⁴

< * < y, czyli odcinek o końcach 0 oraz -y—. Wyznaczymy obraz półpro-

stej L: z = — + iy, 0    < +oo w odwzorowaniu (1.5.26). Ponieważ

4

cos z = y (e^+e^-'¹) więc tym obrazem jest linia o równaniu