matrozw8

194 2. ROZWIĄZANIA I WSKAZÓWKI

Rys. 2.5.4

oo < t < +oo

w =

Obrazem piostej L w tej homografii jest linia o równaniu 1 (1+0 /— 1

2 (1 + 01-2’

Linia ta przechodzi przez trzy punkty

1    7    1

H>1 = W(0) = -, w₂ = Wl-l) = 20 + 20 ' ^oraz

_m 1 ¹ • w₃ = w(l) = j - j i

które nie leżą na jednej prostej. Linia H(L) jest więc okręgiem (tw. 4) bez jednego punktu, a mianowicie bez punktu H (oo), czyli . Ponieważ Re Wj = Re w₃ = |, więc środek w₀ tego okręgu leży na symetralnej odcinka o końcach i vv₃, czyli na

prostej w = —- +iu, -oo < u < +oo. Z warunku I>v_t — Wol = |w₂ — w₀| wyzna-

⁸    ...    3

czarny wartość parametru u, która odpowiada punktowi w₀. Jest nią w = —.

1    3

Stąd w₀ =---1--1. Na rysunku 2.5.5 przedstawiono linię H(L).

8 8

14. Korzystając z tw. 3 (wzór (1.5.6)) otrzymujemy

w—3 z— 1    .    .

-— =-więc w = —z+4

w—2    z—2

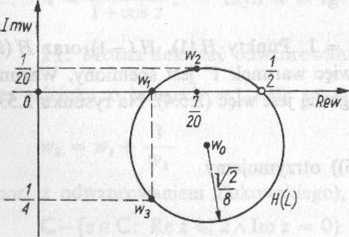
Rys. 2.5.5

Wyznaczona homografia jest odwzorowaniem pierwszego stopnia. Jest ono złożeniem obrotu o kąt (+7t) wokół punktu 0 oraz przesunięcia o wektor [4, 0]. Obrazem okręgu |z| = 1 w tym odwzorowaniu jest okrąg |w—4| = 1. To odwzoiowanie można zilustrować np. tak jak na rys. 2.5.6. Pozostawiam Czytelnikowi narysowanie okręgu |w-4| = 1.

W-,— 2

—m-r 1 1 1	1	2	3	Re z
o>-Co— Łk —
-3 -2 -1 Ó
m '	c"	8"	A"
ó	i	2	3	Rew

Re w Rys. 2.5.6

15. Skorzystamy z tw. 6. Każda homografia (patrz (1.5.8)) 1

^w‘-2 w_t-2 ’

z = 2e'⁸

odwzorowuje koło Iwjl < 1 na koło |z| < 1 tak, że obrazem punktu — jest 0.

0eR

Stąd każda homografia 2z-e¹⁸

^Wt~l=2Sf

odwzorowuje koło |z| < 1 na koło jwj < 1 tak, że obrazem punktu 0 jest .

0e R

v> — 2-

Każda homografia w = 2w_lt czyli 2z-e'⁸

z-2e« ’

odwzorowuje więc (konforemnie) koło |z| < 1 na koło |w| < 2 tak, że obrazem

punktu 0 jest 1. Ponieważ obrazem punktu ~ ma być 0, zatem 1 — e'⁸ = 0, więc 0 =

= 2nk, k = 0, ±1, ±2,.... Stąd szukaną homografią jest 2z— 1

I ^W = ²^2-    <²-⁵-⁵>

Obrazem okręgu 2 |z| = 1 w tej homografii jest pewien okrąg (żadna prosta nie jest zawarta w kole |w| < 2). Znajdujemy obrazy trzech punktów okręgu 2 |z| = 1 w homografii (2.5.5)

w

13*