Nowe skanowanie 20080122080450 00000001D

17. Obwody sprzężone

Impedancja zastępcza

, (Z_t-Z_M)(Z₂-Z_M) ₌    Zi Z₂—Zm

- -^M Z₁₊Z_z-2Z_m    Z₁₊Z₂-2Z_m

co jest zgodne z wyprowadzonym poprzednio wzorem (17.16).

W razie przeciwnego połączenia elementów sprzężonych (rys. 17.1 Ic) otrzymamy układ, równoważny, przedstawiony na rys. 17.1 ld.

Stosowanie opisanych wyżej układów równoważnych ułatwia w wielu przypadkach obliczanie obwodów sprzężonych, a to dzięki zastąpieniu sprzężeń magnetycznych dodatkowymi impedancjami włączonymi w odpowiednie gałęzie.

Przykład 17.3. Wyznaczyć równoważny układ zastępczy gwiazdowy i trójkątowy układu trójkątowego symetrycznego ze sprzężeniami magnetycznymi (rys. 17.12a).

Dane są impedancje: Z = 60+j55 oraz Z\i — jlO.

Rozwiązanie. Pierwsze przekształcenie danego układu przedstawiono na rys. 17.12b, a z konkretnymi danymi liczbowymi — na rys. 17.12c. Impedancje poszczególnych gałęzi w trójkącie wynoszą Z+2Z_M = 60+j75, natomiast impedancje „zewnętrzne” są równe, Z_M = — jlO. Trójkąt na rys. 17.12c zastępujemy gwiazdą, której impedancje są na skutek symetrii trzykrotnie mniejsze. Ostatecznie otrzymujemy równoważny układ gwiazdowy o impedancjach (rys. 17.12d)

Z_x = ⁶⁰-jio = 20+j 15

Odpowiada mu równoważny układ trójkątowy o impedancjach (rys. 17.12c)

Z_A = 3Z. = 60+j45

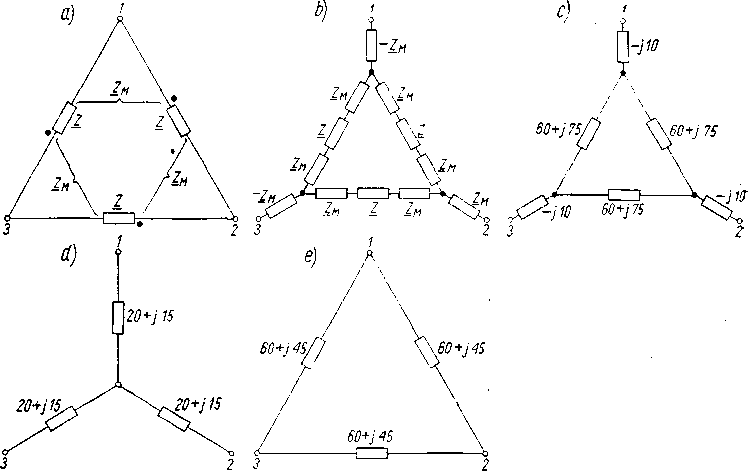
Rys. 17.12. Przekształcenie układu trójkątowego ze sprzężeniami magnetycznymi: a) układ połączeń; b, c, d, e) kolejne przekształcenia (wartości liczbowe odpowiadają przykładowi 17.3)

W ten sposób układ ze sprzężeniami magnetycznymi został zamieniony na równoważne układy (gwiazdowy i trójkątowy) bez sprzężeń.

Gdyby dany układ był niesymetryczny należałoby przy przekształceniach trójkąta na gwiazdę i odwrotnie posługiwać się ogólnymi wzorami stosowanymi przy tego rodzaju przekształceniach.

Pytania

1.    Jakimi równaniami ogólnymi posługujemy się przy rozwiązywaniu obwodów ze sprzężeniami magnetycznymi ?

2.    Na czym polega eliminacja sprzężeń magnetycznych w schematach zastępczych obwodów sprzężonych ? Podać przykłady węzła, w którym zbiegają się gałęzie ze sprzężeniami magnetycznymi.

3.    Opisać przekształcenie układu trójkątowego ze sprzężeniami magnetycznymi na układ trójkątowy bez sprzężeń.

17.5. TRANSFORMATOR BEZRDZENIOWY

Sprzężenie magnetyczne, jak wspomnieliśmy na początku rozdz. 17, może być zastosowane do przeniesienia energii elektrycznej z jednego obwodu elektrycznego do drugiego, jeżeli te obwody obejmują wspólny strumień magnetyczny. Na tym polega zasadnicza koncepcja działania transformatora. Za prototyp transformatora można uważać dwie cewki nawinięte na wspólnym rdzeniu ferromagnetycznym (rys. 17.13a), bądź cewki bezrdzeniowe (rys. 17.13b) umieszczone obok siebie.

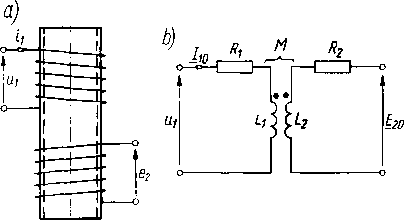
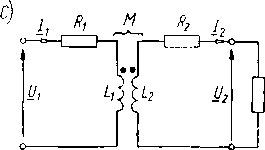
Rys. 17.13. Transformator bezrdzeniowy: a) szkic transformatora; b) schemat transformatora nie obciążonego; c) schemat transformatora bezrdzeniowego zasilanego napięciem sinusoidalnym U_i, obciążonego impedancją Z

Jedną z cewek zasilamy ze źródła o napięciu przemiennym, zazwyczaj sinusoidalnym «!. Wówczas cewka ta wytwarza przemienne pole magnetyczne, indukujące w drugiej cewce napięcie źródłowe e₂, którym można zasilać jakiś odbiornik. W ten sposób powstają dwa obwody odizolowane od siebie elektrycznie, lecz sprzężone magnetycznie. Obwód zasilany ze źródła napięcia nazywamy obwodem pierwotnym, a obwód z nim sprzężony obwodem wtórnym. Odpowiednio do

525