Wyk 25252525B3ad 6 25252525281 2525252529

1

Differenzialrechnuna

1 .Der Beariff der Ableituna

Hinfuhrendes Beispiel. Bei der gleichfórmigen geradlinigen Bewegung geht man davon aus, dass ein Kórper in jeder Sekunde den gleichen Weg zurucklegt. Die Geschwindigkeit wird in diesem Fali durch die Formel

_v _ s_ Zuruckgelegter Weg t Gebrauchte Zeit

festgelegt. Man nimmt also an, dass der Ouotient — konstant d, h, unabhSngig von der Zeit ist.

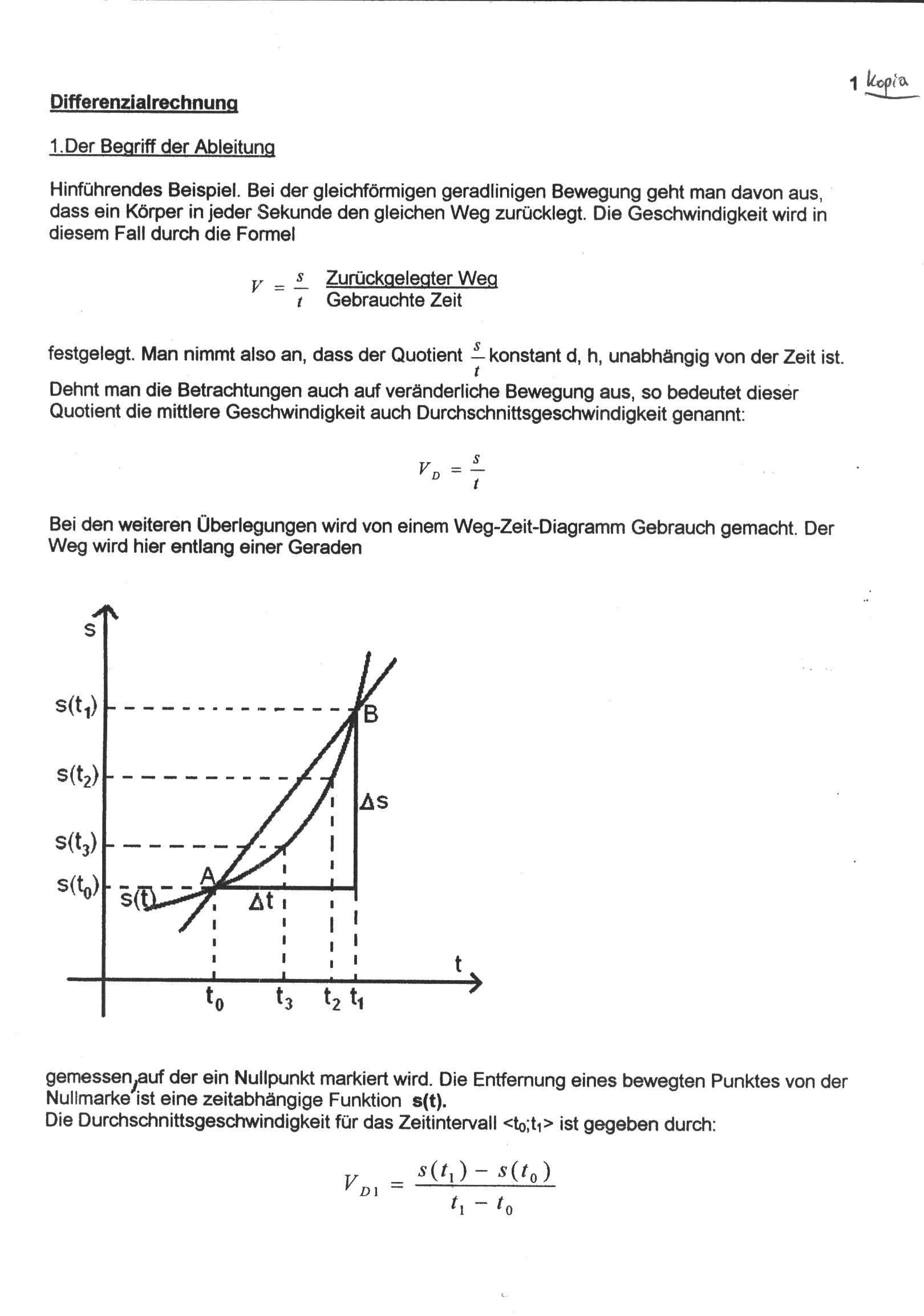
Dehnt man die Betrachtungen auch auf verSnderliche Bewegung aus, so bedeutet dieser Ouotient die mittlere Geschwindigkeit auch Durchschnittsgeschwindigkeit genannt:

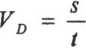
Bei den weiteren Uberlegungen wird von einem Weg-Zeit-Diagramm Gebrauch gemacht. Der Weg wird hier entlang einer Geraden

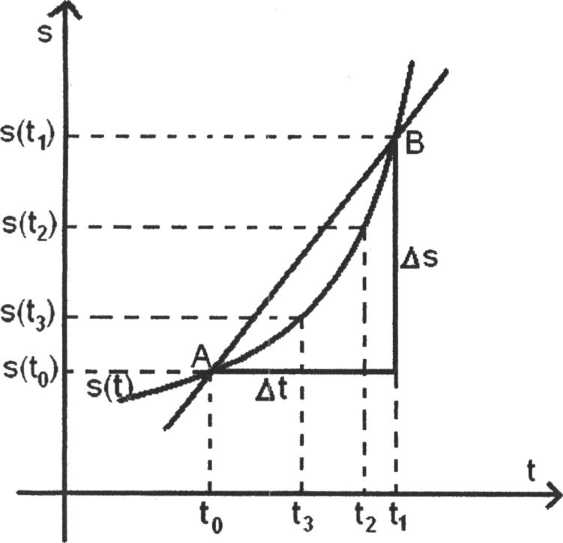
gemessen^auf der ein Nullpunkt markiert wird. Die Entfernung eines bewegten Punktes von der Nullmarke ist eine zeitabhśngige Funktion s(t).

Die Durchschnittsgeschwindigkeit fur das Zeitintervall <to;ti> ist gegeben durch:

_v _ s(hl- ^(^ro)