FizykaII32501

319

Wszystkie te wnioski, wysnute z wzoru (I), nie trudno sprawdzić rysunkiem, śledząc kierunek odbitych promieni w każdym z powyższych wypadków. I tak, gdy MN (Fig. 159) jest prze-

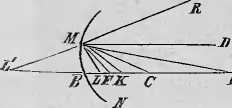
Fig. 159.

cięcie kulistego zwierciadła wklęsłego płaszczyzną, przez oś.jego AB przesuniętą, ,C środek krzywizny, AC główmy kierunek promieni

-d światła, DM promień do tamtego równoległy, który po odbiciu się w punkcie M zwierciadła bierze kierunek MF, wówczas kąt DMC

jest równy kątowi CMF. Lecz DMC = MCF, zatem w trójkącie MCF bok FC— MF. Jeśli tedy punkt M leży bardzo blisko punktu B, można MF— BF położyć; w. takim wypadku oczywiście BF~ t. j. ognisko F leży w połowie promienia BC. Dla Promienia AM, padającego na MN w punkcie M jest kąt padania AMC    BMC, zatem musi także kąt odbicia promienia AM

być mniejszy od kąta FMC, a odbity promień MK przechodzić między ramionami MF i MC kąta CMF i przecinać oś AB w miejscu bardzićj od zwierciadła oddalonem, niż ognisko jego F-zbliżaniem się punktu A do C pomniejsza się kąt padania; dla tego musi się tćż pomniejszać tak samb kąt odbicia, a punkt ^ Przybliżać do C. Gdy A padnie nC, promień padający na zwierciadło w puncie Mjest CM, a kąt padania jest = o, zatćm kąt odbicia — o, a MC wystawia kierunek odbitego promienia, który przez środek krzywizny C przechodzi. Przedmiot i jego °braz schodzą się więc tu razem. Jeżeli świecący punkt stanie " promień KM odbija się w kierunku MA i przecina oś w punkcie A. Promień FM, pochodzący z ogniska i padający w M na zwierciadło, bierze po odbiciu kierunek MD, równoległy do osi zwierciadła, a promień LM, wychodzący z miejsca bliższego zwierciadłu, niż ognisko F, otrzymuje po odbiciu kierunek MB ^z Powodu, że kąt padania LMC~y> FMC, zatćm także odpowiedni mu kąt odbicia CMR j> CMD "być musi. Dopiero więc przedłużenie tego odbitego promienia MB przecina oś zwierciadła ^w Punkcie L'. Wszystkie dotąd wyłożone prawa refl.exyi są ró-"^nie ważne dla świecącego punktu, który nie na osi wklęsłe-§° zwierciadła, ale blisko nićj znajduje się. Gdy bowiem A