page0227

217

WROŃSKIEGO ŻYCIE I PRACE.

z"	>	Z*- J	... 1
	K*+n—i )		...
K*+n+, j	Nfc-f-n )	N*+n-l >	• ■ • N*+«
N* + *»—« )	NH-2n-2 5	fcił-frn—i 1	* * —j

przedstawia czynnik stopnia n-go wielomianu /(x) tem dokładniej, im liczba h jest większą.

⁸) Podajemy w streszczeniu ciekawe wzory matematyczne, odnoszące się do ekonomii społecznej, dodając, że, jak zwykle, podane są u Wrońskiego bez dowodu. Zasadnicze określenia przytoczone są już w tekście.

»Przyrost ekonomiczny* a jest funkcyą czasu; funkcya ta, według Wrońskiego, czyni zadość równaniu różniczkowemu

doc. = a { 0*“¹ ‘ — 1} _;

gdzie 0 jest także pewną funkcyą czasu, o której zaraz będzie mowa.

Wzór na da można napisać w postaci:

den — a dt

log 0 —B

7 n dhog 0 1.2    ³ dt*

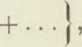
d log 6

¹ dt

+—-5₂

d^Q log 0

dt*

gdzie B_x , B.,, B₃.... są liczby Bernoulliego.

Funkcyi 0 nadaje Wroński a priori jeszcze postać następującą: gdzie A, x, X, ja , v, ... są pewne stałe, określone przez warunki ekonomiczne społeczeństwa i dające się oznaczyć za pomocą doświadczenia, a mianowicie ze związku:

R — $(R — P) _ _t + +    + p<^s +

P

biorąc rozmaite wartości sił P i R i odpowiednią wartość [3, (t. j. część zysku społecznego, jaka się zużywa) i układając tyle równań, ile jest ilości niewiadomych.

W warunkach zwykłych 0 ma być stałe, wtedy x = X = p = v= ... = 0, i otrzymamy

a = A*.

Przyrost społeczny tworzy tedy postęp geometryczny względem czasu. „Z tego widać, powiada Wroński, jak błędnem jest z jednej strony zdanie Malthusa, który ten postęp geometryczny sprowadzał do prostego postępu arytmetycznego, z drugiej zaś, jak źle uzasadnionem jest roszczenie Proudhona, który opierając się na poglądzie Malthusa, chciał znaleść zasado destrukcyi porządku ekonomicznego społeczeństwa".

>Konkurencyę ekonomiczną* 6 określa Wroński za pomocą wzoru

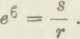
gdzie e jest podstawą logarytmów Neperowych, » — praca ofiarowana, t. j. podaż, r — praca poszukiwana — t. j. p“o pyt. Z wzoru tego wynika

.<!

^ —* log

http://rcin.org.pl