0297

299

§ 5. Szeregi iterowane i podwójne

Będziemy badali tylko takie szeregi, dla których tego rodzaju punkty M* istnieją. Inne szeregi nie są dla nas ciekawe. Sam charakter lematu pozwala nam ograniczyć się do rozpatrywania tylko pierwszej ćwiartki układu współrzędnych. Otrzymane wyniki można przez symetrię rozszerzyć łatwo na pozostałe ćwiartki.

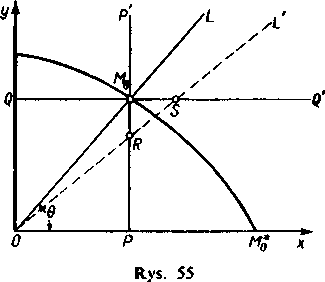
Weźmy w pierwszej ćwiartce półprostą OL wychodzącą z początku współrzędnych pod kątem 9 do osi x (rys. 55). Tak samo, jak w 379, korzystając z lematu można udowodnić, że istnieje taka liczba dodatnia R (0) (może to być także nieskończoność), że we wszystkich punktach M tego promienia, dla których

OM <R (9),

szereg (14) jest bezwzględnie zbieżny, podczas gdy dla punktów M, dla których

OM > R (8), szereg jest rozbieżny.

Jeżeli dla chociażby jednego promienia jest R(6) = +oo, to na mocy lematu szereg jest zbieżny i do tego bezwzględnie na całej płaszczyźnie, która jest wtedy obszarem zbieżności 97?.

Wyłączymy teraz przypadek szeregów wszędzie zbieżnych. Wówczas R (9) będzie funkcją skończoną zmiennej 9 i na każdym promieniu L znajdzie się punkt rozgraniczający M_e, dla którego

0M_e = R (9).

Oddziela on te punkty M promienia, w których szereg jest bezwzględnie zbieżny, od tych w których szereg jest rozbieżny. W samym punkcie M_e zależnie od szeregu, może on być albo zbieżny, albo rozbieżny.

Jeżeli poprowadzimy przez M_e prostą pionową PP' i poziomą QQ' (patrz rysunek 55),. to wewnątrz prostokąta OPM_t Q szereg jest na pewno zbieżny, a wewnątrz kąta Q' M_e P' jest na pewno rozbieżny (na mocy lematu). Na nowym promieniu OL', odpowiadającym jakiemuś innemu kątowi 9', szereg jest zbieżny na OR i rozbieżny na SL', a zatem punkt, rozgraniczający M₉, na tym promieniu musi leżeć między R i S. Łatwo stąd zauważyć, że gdy 9 zmienia się od O do tc/2, funkcja R (9) zmienia się w sposób ciągły, a więc punkt M_t zakreśla w pierwszej ćwiartce pewną ciągłą krzywą rozgraniczającą.

Ponieważ gdy zmniejsza się 9, odcięta x_e punktu M„ nie maleje, a rzędna y„ nie rośnie, więc mają one wartości graniczne, gdy 9 -* 0. Ma więc oczywiście granicę także R (0). Jeśli ta granica

lim R (0) = R₀

9-0

jest skończona, to punkt M_e dąży do pewnego punktu granicznego M*{R₀, 0) na osi x, w przeciwnym razie rozgraniczająca krzywa ma asymptotę równoległą do osi x, która może się ewentualnie pokrywać z tą osią. Łatwo odpowiednio pozmieniać wysłowienia dla przypadku, gdy 9 -> 7r/2, zmieniając role zmiennych x i y.