0285

287

§ 5. Szeregi iterowane i podwójne

Twierdzenie 3. Dam jest macierz (1). Jeżeli po zastąpieniu wyrazów szeregu (3) ich wartościami bezwzględnymi otrzymuje się zbieżny szereg, to obydwa szeregi iterowane (3) i(4) są zbieżne i mają tę samą sumę:

00 00    00 0Q

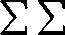
*—i i-i    i-i i-i

394. Szeregi podwójne. Z nieskończoną macierzą prostokątną (1) jest związane także pojęcie szeregu podwójnego. Tak nazywa się symbol

	a?>+a?+a?>+	... +a^+ ..
	+ a\^2)+a2^2) + a^(3^2) +	... +a\^2)+ ..
(10)	+ a^i? + aF + a?+ .	,. +flr+...

+........................- E

(, k-/

Ograniczając się do m pierwszych kolumn i n pierwszych wierszy, rozpatrzymy skończoną sumę

i—m, k—n

AS'- £ «!¹’,

I. k-1

która się nazywa sumą częściową danego szeregu podwójnego. Będziemy zwiększali liczby m i n do nieskończoności, ale niezależnie od siebie. Skończona lub nieskończona granica

A = lim AiT¹

m-¹oo n—oo

nazywa się sumą szeregu podwójnego; piszemy

.4= t <>!"•

ł, k-1

Jeżeli szereg (10) ma sumę skończoną, to nazywa się zbieżny, w przeciwnym razie — gdy nie ma sumy lub ma sumę nieskończoną — rozbieżny.

Wróćmy na przykład do macierzy (7) z poprzedniego paragrafu, o wyrazie ogólnym

cr = Aj ’^k •

W tym przypadku suma częściowa jest oczywiście równa (jeżeli zachowamy dawne oznaczenia)

C^w = A R

'■'m ^Am °n >

a więc szereg podwójny odpowiadający tej macierzy jest zawsze zbieżny i ma sumę

C = lim A_m B„ = AB (¹)

m-+ oo w-¹oo

1

Jeżeli zatem przedstawimy iloczyn dwóch szeregów zbieżnych w postaci szeregu podwójnego, to sumą tego szeregu będzie zawsze AB. Trudność polegała na dowodzie tego samego dla iloczynu przedstawionego zwykłym szeregiem.