037 bmp

Korzystając kolejno z prostego i odwrotnego przekształcenia Laplace’a w zależności (6.5), otrzymamy przebieg czasowy odpowiedzi

H0 = .Z'V [*(0]G(_S)}    (6.6)

gdzie:    J - proste przekształcenie Laptacc’a wyrażenia w nawiasie,

J~^] - odwrotne przekształcenie Laplace’a wyrażenia w nawiasie.

Znalezienie oryginału y(t) z zależności (6.6) sprowadza się do korzystania z tablic przekształceń Laplace'a.

Jeżeli transmitancja jest funkcją złożoną, trzeba ją uprzednio przekształcić do prostszej postaci, stosując znane z matematyki wzory Heaviside’a. Należy podkreślić, że równanie w postaci operatorowej zawiera warunki początkowe, dzięki czemu uzyskuje się pełny przebieg czasowy oryginału bez konieczności wyznaczania oddzielnie stałych całkowania.

Zgodnie z równaniem (6.5) własności dynamiczne przetwornika będącego stacjonarnym układem liniowym jednoznacznie określa transmitancja operatorowa Gis), która nie zależy od sygnałów wejściowych ani wyjściowych, a jedynie od charakteru równania operatorowego wynikającego ze struktury przetwornika i parametrów układu przetwornika.

Znajomość transmitancji operatorowej przetwornika umożliwia wyznaczanie sygnału wyjściowego w' stanie przejściowym wywołanym zmianą amplitudy sygnału wejściowego. Dla przetwornika o danej transmitancji operatorowej można również określić przebieg sygnału wyjściowego w stanie ustalonym przy sinusoidalnej zmienności sygnału wejściowego. Wiadomo z matematyki, że korzystając z przekształcenia Fouriera, sygnały periodyczne lub nieperiodyczne opisane funkcjami spełniającymi warunki Dirichleta (w praktyce wszystkie przebiegi dające się zrealizować fizykalnie są opisane takimi funkcjami) można przedstawić w postaci przebiegów harmonicznych.

Przy wyznaczaniu wpływu własności dynamicznych przetwornika na sposób przenoszenia przez niego sygnałów harmonicznych w stanie ustalonym korzysta się z transmitancji widmowej G(/0)), która jest szczególnym przypadkiem transmitancji operatorowej, gdy a = 0, wówczas

(6.7)

Transmitancja widmowa wyrażająca stosunek transformat Fouriera sygnałów wyjściowego 7(/co) i wejściowego Aijto) jest funkcją zmiennej zespolonej i może być wyrażona w postaci kanonicznej

GC/co) =

Y(M

(6.8)

Wprowadzając interpretację geometryczną zmiennej zespolonej na płaszczyźnie współrzędnych prostokątnych (P, jQ), moduł transmitancji widmowej wyrażonej związkiem (6.8) określa wzór

G(a>) = |G(yco)| = Jp¹ (co)+Q² (w)    (6.9)

cp(to) = arg[G(yo))] = arctg—-

(6.10)

Transformaty Fouriera harmonicznych sygnałów: wejściowego X(jto) i wyjściowego 7(/'0)) wyrażone w formie wykładniczej przy wykorzystaniu znanych z matematyki wzorów Eulera można zapisać następująco:

X(j<s)) = X_m[cos(w + <p J + ysin(atf + <p J] =

= X_me^i{^\

(6.11)

Y(j®) = y.[cos(fljr + <p„) + j sin(tot + ę_y)] =

_ y _e’^{<s*^y^]

W tym przypadku transmitancję widmową przedstawia wyrażenie

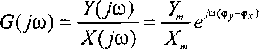
(6.12)

Z (6.12) wynika fizyczny sens modułu transmitancji: |G(jca)| = Y_m!X_m, który wyraża wartość

stosunku amplitud harmonicznego sygnału wyjściowego i wejściowego oraz argumentu transmitancji: cp((o) = tp _y - (p^ będącego różnicą faz sygnałów wyjściowego i wejściowego.

Transmitancję widmową zwykło się przedstawiać za pomocą charakterystyk częstotliwościowych, z których dla celów metrologicznych najczęściej wykorzystuje się charakterystyki:

-    amplitudową [G(jO))[ = G(to), która określa zależność stosunku amplitud harmonicznych sygnałów wyjściowego i wejściowego od pulsacji a) sygnału wejściowego,

-    fazową (p((o), która wyznacza zależność między wartością różnicy kątów fazowych harmonicznych sygnałów wyjściowego i wejściowego apulsacjąco.

Wykresy tych charakterystyk wykonuje się często w skali logarytmicznej; dotyczy to pulsacji w w^r obu charakterystykach oraz modułu |G(y'co)j w charakterystyce amplitudowej, przy czym wprowadza się tu pojęcie modułu logarytmicznego transmitancji

(6.13)

Lm [G(/co)]= 201g|G(y'co)|

1.Jednostką modułu logarytmicznego jest decybel dB, na przykład dla |G(yco)| = 100, Lm[G(j(ti)] = Zm(co) = 40 [dB]. Dwukrotna zmiana pulsacji w skali logarytmicznej nazywa się oktawą, zaś dziesięciokrotna - dekadą.

75