0405

407

§ 3. Zastosowania

a następnie różniczkujemy otrzymany szereg wyraz za wyrazem:

ri— 1

Ponieważ majorantą szeregu pochodnych* jest ciąg geometryczny zbieżny, więc różniczkowanie wyraz za wyrazem jest uzasadnione.

9) W 408 wprowadziliśmy rozwinięcie sin x w iloczyn nieskończony

sin x — x

n-l

Biorąc wartości bezwzględne otrzymujemy stąd

|sin*b=

nm 1    ¹

Jeśli x jest różne od liczb postaci kn (k = 0, ± 1, ±2...), to logarytmując otrzymamy szereg nieskończony

In fsin x| = ln |jr| + lnll--7—

I n²n²

n— 1

Różniczkując wyraz za wyrazem otrzymamy następujące rozwinięcie:

££ii ₌ c.g^ = ±+y-_r2£_rr.

sin x    x £—i x² — n²n²

fl— 1

Dla uzasadnienia takiego postępowania wystarczy się przekonać, że otrzymany szereg jest zbieżny jednostajnie w dowolnym przedziale skończonym domkniętym, nie zawierającym punktów postaci kn. Rzeczywiście, gdy x pozostaje w tym przedziale, jego wartość bezwzględna jest ograniczona \x\<M, więc (przynajmniej dla n> M/n) zachodzi nierówność

2x

2M

=    ² W <

nhr²-W^J    n²n²-M²

Ponieważ szereg

CO

E

H> M/Tt

2M

n²n² — M²

jest zbieżny, więc żądany wynik otrzymujemy korzystając z kryterium Weierstrassa. Rozwinięciu ctg x można nadać postać

= Ctg X

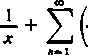
-rm x+nn /

cos x sin x

w tej postaci jest ono jak gdyby rozkładem ctg x na ułamki proste odpowiadające poszczególnym pierwiastkom 0 i +rm mianownika sin x.

Ze wzoru tg x = —ctg (x— y 7t) można otrzymać rozkład tg x na ułamki proste

tgx =

CD

-El

_j_

2n— 1

2

, 2n—1 XĄ--n

2

00

l—E-

r²-

2x

(2it-l)²n²

4