0606

608

XIV. Całki zależne od parametru

Wynik ten otrzymamy od razu całkując szereg wyraz za wyrazem

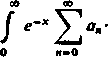
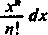
00 00 Żt/

■x"dx

Z

a.

n»0

»

ponieważ J e~‘x"dx = ni [489, 4)]. Pokażemy teraz, że całkowanie takie jest tu dozwolone.

O

Podobnie jak w poprzednim przykładzie, w skończonym przedziale możemy tu całkować wyraz za wyrazem

(10)

Całkując przez części stwierdzamy łatwo, że

—5— r ^e~^x'*’dx <--- f e~*x"~'dx < 1

ni J    (n-l)i J

Wobec tego czynniki

A

— f e~^xx"dx , n! J o

zależne od A i n, są wspólnie ograniczone dla wszystkich A i n oraz — przy stałym A — maleją monofonicznie wraz ze wzrostem n. Szereg z prawej strony równości (10) jest zatem, na podstawie wspomnianego wyżej kryterium Abela, zbieżny jednostajnie względem A. Można tym samym przy A -*■ oo przejść w nim do granicy wyraz za wyrazem.

Przytoczymy dwa przykłady zastosowania eleganckiego wzoru (9).

(a) Rozpatrzmy tak zwany sinus całkowy

00

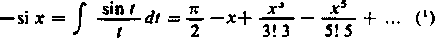
x

Szereg ten możemy utworzyć tak jak szereg g (x) wychodząc z szeregu

2L_l₊0+-i-+0--i-+ ...

2    3    5

Z wzoru (9) otrzymujemy teraz

- f e~^xsixdx=——(l—— + —--—— — = —.

^Jn    2\35    /    244

(') Łatwo jest wyprowadzić to rozwinięcie pisząc

__siJe= f -§i2±rf,-

j    t j    t

o    o

zastępując następnie w drugiej całce sinus jego rozwinięciem na szereg i całkując wyraz za wyrazem.