0667

§ 5. Całki Eulera

669

Stąd

_A _ (y-») (y-P) _c

y(y-x-p)

Rozpatrzmy teraz wyrażenie

(32)

/?. y, l)

r(y-<%) T(Y-ff) r(y) Tiy-z-P)

poprzednia równość, wobec (9), pokazuje, że wartość tego wyrażenia nie ulegnie zmianie, gdy zamiast y napiszemy y+m. A więc

F(x,p,y, 1)

r(y+m — a)-r(y+m — P) r(y+m)-r(y+m—tx—p) ’

r (y—a)' r (y—fi)

r (y)' r (y—<x—p)

= F(x, p, y+m, 1)

Przejdźmy w prawej stronie tej równości do granicy przy m    oo. Z tego, że szereg F (*, p, y+ m, 1) jest

zbieżny jednostajnie względem m, wynika [433], że suma jego dąży do 1. Równa 1 jest także granica czynnika

r (y+m—ot)-r (y+m —P) r(.y+m) r(y+m—x^P) ’

ponieważ jest on równy iloczynowi otrzymanemu przez odrzucenie m— I początkowych czynników zbieżnego na mocy 5) iloczynu nieskończonego

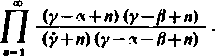
Tak więc wyrażenie (32) jest równe 1, a to jest równoważne z wzorem Gaussa. Przyjmując w tym wzorze y = 1, * = P= —j można otrzymać rozwinięcie

1 +

(ł)’+(&)*+«+(

1•1•3-5 \ 2-4-6-8Z

2

+ ...

±

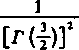
TZ

Można też otrzymać ogólniejszy wynik, a mianowicie można udowodnić, że suma współczynników dwu-miennych w przypadku, gdy m jest wykładnikiem potęgi dwumianu, jest dla m > —'₂ równa

r(l+2m)

[r(l+m)]^J

(y = 1, * = P = -m).

Przedtem nie mogliśmy uzyskać tego wyniku, ponieważ krępował nas warunek a. > 0.

8) Rozszerzenie funkcji r(a) na ujemne wartości a. Zgodnie z wzorem (9) jest

/’(«) =

r(a+1)

a

a więc wartość Z’(<z) jest określona przez wartość F (o+1). Jeśli —1 <0<O, to 0+1 >0 i symbol r(a+l) ma sens. Niech teraz powyższy wzór będzie określeniem wartości /'(a); w ten sposób określenie funkcji r (a) będzie rozszerzone na przypadek — 1 <a<0. Ogólnie, jeśli — n<a< — (n— 1), to rozszerzając zakres wzoru (10) na te wartości zdefiniujemy r (a) przez równości

(33)

r(a)--F(a+n)-

0(0+1) ...(0+/1-I)

Napiszmy dla większej przejrzystości a= — n+a, gdzie 0<«< 1; teraz powyższą definicję możemy napisać tak

(34)

r(a)

(l-*)(2-*) ...(n-<x)