82416

Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWU 13
|
In |
1 2 |
Ad 2. Rozpatrzmy teraz przypadek, gdy tłumienia są duże p> w (tłumienie nadkrytyczne). Wówczas również otrzymujemy dwa rozwiązania (tym razem rzeczywiste) równania charakterystycznego:
r,=-p-\p‘-(o'
—_- (12.29)
r,=-p+vp*-o>*
Funkcja rozwiązująca dla tego przypadku ma następującą postać:
g(/)-e""(Ć ,-sinhiB,t+Ć 2cosh&,t) (12.30)
Na rys. 12.12 przedstawiono wykres funkcji rozwiązującej (12.30).

Rys. 12.12. Funkcja ro^viqptjqca <tłumienie fiadkrytyczne)
Z lys. 12.12 wynika, że drgania z tłumieniem nadkiytycznym szybko zanikają i nie mają charakteru oscylacyjnego. Częstość kołowa digaii własnych wynosi:
i0,=\p2-w: (12.31)
Ad 3. W przypadku tłumienia krytycznego, tzn. gdy p=co. rozwiązanie pizyjmuje postać funkcji:
AlmaMater
Dobra D.. Dztakicwlcz L, Jambrożrk S.. Kotnona M.. Mikołajczak K.. Przybylaka P., Sytak A.. Wdowdca A
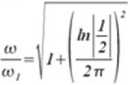
Wyszukiwarka
Podobne podstrony:
Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWU 10 Część 2 12. WPROWADZENIE DO DYNAMIKI
Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWU 15 Część 2 12. WPROWADZENIE DO DYNAMIKI
Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWU 6 Przykład 2 Znaleźć częstość kołową drgań
Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWU 2 Rys. 12.1. Układ o jednym stopniu suobody dyitomi
Część 2 12. WPROWADZENIE DO DYNAMIKI BUDOWLI 17 i dalej na podstawie (12.34): m t/(t)+c (i[t)+k
Wprowadzenie do wydania polskiego 13 W porównaniu z wydaniem pierwszym z 1993 roku ostatnie wydanie
12 Wprowadzenie do wydania polskiego ekonomicznym jak działalność podmiotów gospodarczych w sferze
Laboratorium 5-8 Symulacja ciągła Wprowadzenie do dynamiki systemów
Częsc pierwsza. Wprowadzenie do problematyki psychologii zeznan Carl von Eckartshausen znany jest pr
Częsc pierwsza. Wprowadzenie do problematyki psychologii zeznan psychologia sądowa rozpłynęła się ja
Częsc pierwsza. Wprowadzenie do problematyki psychologii zeznan (czynnik „p”). Przewaga czynnika
Częsc pierwsza. Wprowadzenie do problematyki psychologii zeznan podstawowym kierunkiem eksperckiej p
więcej podobnych podstron