0049

51

§ 3. Całkowanie pewnych wyrażeń zawierających pierwiastki

I tym razem otrzymaliśmy poprzedni wynik tylko w innej formie, ponieważ zachodzą tożsamości

— 2arc tg

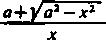
arcsin——n    dla 0 < x < a,

a

arcsin— +n dla — a < x < 0. a

D f-jĄ

J y _L ł/v*

dx

x+^x²—x+l

(a) Zastosujemy najpierw pierwsze podstawienie ]/x²—x+l = t—x; otrzymamy

x =

t¹-1

2/ — 1 ’    ""    (2/— l)²

f dx    r 2t²-2t+2 _ds f T 2    3    3    1 _±

J _x+y:_rT-__JC+1 J r(2r-l)^ł JLr    2r—I    (2t-l)²J

-4--^-r⁺²¹ⁿ m-4^ln 12/-11+C. 2 2/-1 2

Jeżeli podstawimy tu t — x+^x²—x+l, to otrzymamy ostatecznie

f dx ₌ _ _3_ _1__

•’ x+]/x²-x+\    2 ' 2jt+2yGr²-*+l-l

— -|-2 ln |2*+2^jc²—jc+1 —1| +21n |jc+|/jc²—jc+ 1| + C.

(b) Zastosujemy teraz drugie podstawienie: ^x²—x+l = tx—l, mamy

'^2-'+l d, (»*-!)* ’	Yx^2-	^+ ,^2_1 ’	x+^x^2-x+\ =-p-j-.
— 2/^2+2f—2	■dt-	r[2 i.i	3.1 3 ]df
+ 1		I L* 2 /— 1	2 r+i (»+l)^2J"'

³    +21n |r|—Ł-ln |/—1|—-|-ln |r+l| + C'.

/+!

i/ x²—14“ 1

Pozostaje teraz podstawić t — ⁹    i po oczywistych uproszczeniach otrzymujemy

f /- —    ~ = — :-- +2 ln \yx²— jc+l + l|—

^J x+tfx²-x+l    |/jc²—jc+ 1+jc+ 1

- y ln ||/jc²—jc+1—jc+l| - ln |y'V-*+l f x+l| 4- C'.

Wyrażenie to chociaż różni się kształtem od otrzymanego wyżej, jednak pokrywa się z nim, gdy C'=C+j