10

12 A.S, ,lM,-icllo, Systemy elektromechaniczne dla elektryków

d_dL

dt dq_{

dL

--W,-^c_f = 0 1 = 1.....n

(2.8a)

Y_J^cjńi^+cjto^:=0 j =    (2.8b)

1=1

Należy w tym miejscu zauważyć, że opisaną powyżej metodą można także rozwiązywać zagadnienia dynamiki układów, w których występują więzy niecałko-walne liniowe. Posługiwanie się jednak powyższą formułą przy rozwiązywaniu układów z więzami kinematycznymi jest w tym sensie niewygodne, że powiększa liczbę niewiadomych o liczbę współczynników nieoznaczonych Lagrange’a. Zauważmy, że jeżeli równanie więzów (2.8b) można przekształcić do postaci:

n

9j=    1’--’?/.)?/’ j = U —    (2.9)

i=m-fl

to eliminując zmienne zależne, można po zmodyfikowaniu funkcji Lagrange’a wykorzystać równania Lagrange’a drugiego rodzaju - (2.3). Problem się jednak komplikuje, gdy równanie więzów (2.8b) można przekształcić jedynie do postaci:

n

i=/»+l

gdzie współrzędnych q_k nie można zaliczyć do żadnej z grup o indeksach od jeden do n. Powyższe równanie nie jest równaniem całkowalnym, bowiem nie spełnia warunku całkowalności Pfaffa. Wygodniejszym dla dalszych rozważań zapisem powyższych równań więzów jest postać:

S

Qj~~ 'y i ^'ji faCk 15 • • • 5    ) Qi ’ J ~ b • • • > 5 k —    S

i=1

lub

s

⁵3y = Z^Cyife«>-"’5Ci_!)8a. j = l.....    (2.10)

/=!

Wykorzystując relację daną wzorem (2.10), w równaniu (2.1) otrzymujemy [4]:

d dL dL

1 ^s dL

Qt *-i

(2.11)

Dla przypadku maszyn elektrycznych z komutatorem mechanicznym lub elektronicznym powyższe równanie modyfikuje się do postaci:

d dL dL

'dtdS'^

j dL Qi *-i3(a-Tu)

k=\

k = 1,

5    (2.12a)

(2.12b)

d dL dL ₊ * dL _ j,

dt di} dft k=i 9('ó-rb)

Należy w tym miejscu zaznaczyć, że jako 5 w powyższych równaniach oznaczona jest liczba niezależnych par szczotek w przypadku komutatora mechanicznego, natomiast dla komutatora energoelektronicznego oznacza liczbę obwodów pośredniczących.

Rozważmy teraz wyrażenia na energię kinetyczną, potencjalną, a także na energię zawartą w polu magnetycznym i elektrycznym. Ogólnie przez energię rozumie się zdolność ciała lub układu ciał do wykonania pracy, można zatem wyrazić jł\ wzorem:

m

* = Ej Ffy    (2.13)

j=1

Jeśli dobrać współrzędne układu tak, aby kierunki wektorów sił lub ich składowycli pokrywały się z tymi współrzędnymi, to relacja (2.13) przyjmie postać:

E =

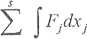
j=i

(2.14)

Wyrażenie (2.14) bezpośrednio określa energię potencjalną, jeśli tylko siły Fjsą stałe lub zależą wyłącznie od współrzędnej położenia Xj. Jeśli natomiast siły te si\

wynikiem przyspieszenia lub odwrotnie - przyspieszenie jest wynikiem działających sił, to wykorzystując drugie prawo dynamiki Newtona, możemy napisać:

= (^2J5)

j=l ^al    j=1

gdzie:

E_k - energia kinetyczna układu,

_ ^dxj

^Vj dt ’

p,    j-ty pęd układu (pęd y-tego punktu materialnego lub y-ta składowa

tego pędu).