165

A HibUl. IM1U.1 ,Vv»«    r ), buui :uO

ISBN D4H1II ł-7. © l>. WN TOS >«}

5 2 PUNKTOWE GRUPY SYMETRII

ltó

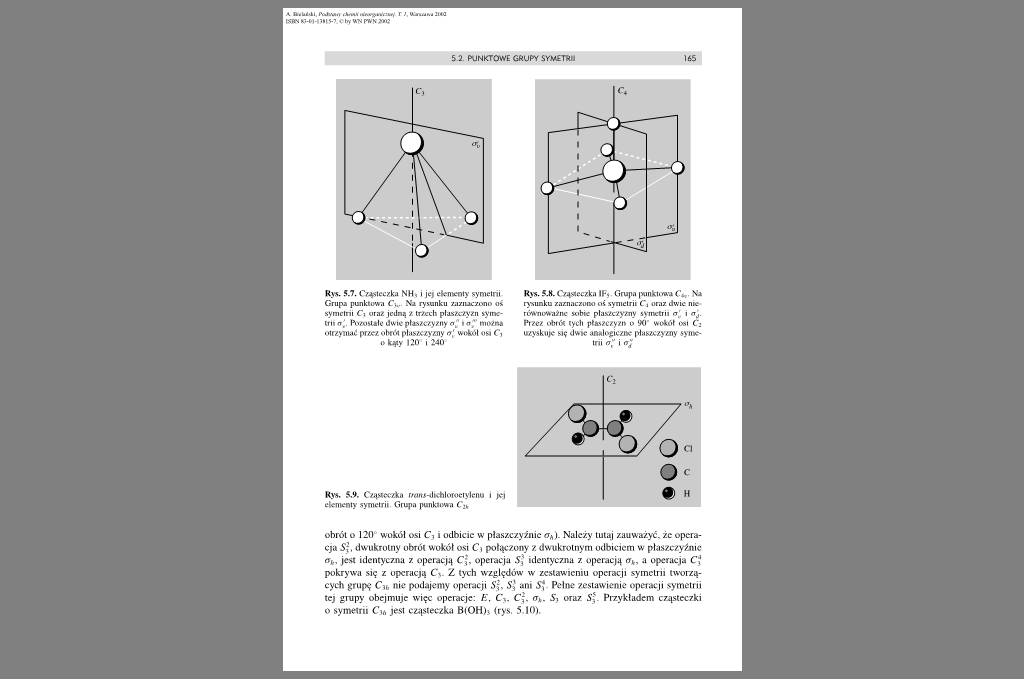
Rys. 5.7. Cząsteczka NH, i jej elementy symcini Grupa punktowa Ci... Na rysunku zaznaczono ot symcini Ci ant jedną Z trzech płaszczyzn symetrii o'. Pozostałe dwie płaszczyzny a" i o '' można otrzymać przez obrót płaszczyzny <»,' wokół om Oj okąiy 120 i 240

Rys. 5.8. Cząsteczka Ib. Grupa punktowa C*,. N'a rysunku zaznaczono o i symetrii C, oraz dwie nie równoważne sobie płaszczyzny symetrii o.' i Oj. Przez obrót tych płaszczyzn o 90 wokół osi Ć-uzyskuje się dwie analogiczne płaszczyzny symetrii rrj i oj

Rys. 5.9. Cząsteczka r/tws-dKłilorociylcnu elementy symetrii. Grupa punktowa C-s

	c.
/J	kz:
	O^c 9) H

obrót o 120 wokół osi C, t odbicie w płaszczyźnie <r_A). Należy tutaj zauważyć, że operacja S;. dwukrotny obrót wokół osi Ci połączony z dwukrotnym odbiciem w płaszczyźnie a_b, jest identyczna z operacją Cf, operacja 5,' identyczna z operacją rr_v. a operacja C‘{ pokrywa się z operacją t\. Z tych względów w zestawieniu operacji symetrii tworzących grupę Cjł nie podajemy operacji 5;. 5, ani S* Pełne zestawienie operacji symetrii tej grupy obejmuje więc operacje: E. C\. Cj. tr*. S, oraz S|. Przykładem cząsteczki o symetrii Cu, jest cząsteczka BlOH). (rys. 5.10).