Strona1 (2)

Rozdział 17

CAŁKI POWIERZCHNIOWE

17.1. CVtKA POWIERZCHNIOWA NIEZORIENTOWANA

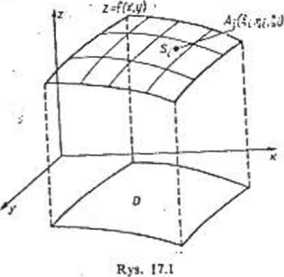
Definicja całki powierzchniowej niezorientowanej. Niech będzie dany płat powierzchniowy regularny S (por. T. I, rozdz. 12.8) o równaniu:

(1.1)    z=f{x,y) dla (x,y)eD,

gdzie: Z) jest obszarem płaskim regularnym ograniczonym jedną krzywą zamkniętą (rys. 17.1). Powierzchnię 5 dzielimy na n dowolnych części: S_L, S₂, ..., S,_„ Oznaczmy pola tych części odpowiednio przez: AS_lt AS₂,..AS_M-_U AS„ oraz przez

= 4,(Źit Hh Cr) dowolnie wybrany punkt należący do części 5,-, czyli A,eS₍ (i 1, 2,.... ;i). Niech F(x, y, z) będzie funkcją określoną i ograniczoną na płacie regularnym 5 o równaniu (1.1). Tworzymy sumę całkową <r, postaci:

(1.2)    f G*_t) AS_t    F(/f_:) AS₂ + ... + F(A.) AS_ą.

gdzie: F(A,) - F(Ę/, 7/. Cii-

Jcicli istnieje granica skończona ciągu sum (o*) przy założeniu, że n dąży do nieskończoności oraz wszystkie średnice części S, dążą do zera i gdy granica ta nic zależy od sposobu dzielenia powierzchni S na części i od wyboru punktów A, w tych częściach, to granicę tę nazywamy całkę powierzchniową niezorientowana funkcji F(x, y, z) po piacie regularnym S i oznaczamy symbolem:

(1.3)    SJ/Tr, y.z)dS. '

s

Twierdzenia o zamianie całki powierzchniowej niezorientowanej na zwykłą całkę podwójną.

Twierdzenie 1. Jeżeli funkcja F(x, y, z) jest ciągła na płacie regularnym S o równaniu (1.1), to całka powierzchniowa niezorientowana (1.3) istnieje i wyraża się wzorem:

o-4);

i S r(x. y, z) dS - i\F[x, yj(_x, >•)] V l i/j^:(.r.y) 4 f;'(x, y) dxdy. s    o

gdzie: D jest obszarem płaskim regularnym będącym rzutem płata S na płaszczyznę Oxy. Uwaga I. Wzór (1.4) dla płaUt powierzchniowego ó' o równaniu typu:

(I O

lub

on

przyjmuje odpowiednio postać:

^x = Sb\ ;) dla (y.d)cD_t, y = Jt(x, :) dla (ar, r) c0>

0-4')

lub

d.4") •

$1    =    -).>*. r]/l r g^,/(y,=)+'i:ⁱ(y,:)dyd;

s    r»i

S ! ^F(x. )\ -) dS j $ F[x, h {X, z), z] V 1 -f h; (x, z) ■{ h} (x, z) dx dz. ⁵    p>

Uwaga 2. Wzory (1.4), (1.4') i (1.4") stosuje się w przypadku płatów regularnych odpowiednich typów. W celu obliczenia całki (1.3) po dowolnej powierzchni regularnej należy ją rozłożyć na sumę skończonej ilości płatów regularnych i do każdego z nich zastosować jcdca z w/orów (1.4), (1.4') lub (1.4").

Definicja. Powierzchnię S o równaniach parametrycznych;

ix = .v(i/, v)

y =    v), gdzie (u, \ )cd,

- =

nazywamy piatem powierzchniowym Te^ularn)m. jeżeli spełnione są następujące warunki:

87