PC043397

106

Pierwiastkami funkcji wymiernej f(x) => Jgi _Są tc liczby, dla lufo, W{x) - O i jednocześnie G(x) * O, czyli liczby ze zbioru {xe D_f : W(x) =*0}

Przykład 1.98

W celu wyznaczenia pierwiastków funkcji f(x) = jc³±s~-4*. należy najpieitw znaczyć jej dziedzinę. Funkcja /jest określona na zbiorze:

Df= {x eU:x^z-9#Q} = R\{-3,3>.

Miejscami zerowymi będą te argumenty należące do zbioru D_f, dlak%' licznik funkcji /się zeruje, tzn. X³ + X² - 6x = 0. W celu rozwiązania otrzy* nego równania wyłączamy czynnika przed nawias, a następnie, wykorgsSj wzory na pierwiastki równania kwadratowego, otrzymujemy rozwiąż^: % = -%Xi = 0 oraz X} = 2. Pamiętając jednak o dziedzinie funkcji /, musw odrzucić rozwiązanie x, = -3 jako to, które nie należy do dziedziny. Żale? funkcja f posiada dwa miejsca zerowe: O i 2.

Funkcja fiomograficzna

Szczególnym przypadkiem funkcji wymiernej jest funkcja postaci:

/(*) =

ax+b cx + d

(i.nv

dla od - bc ± 0 i c * 0, zwana funkcją homograficzną.

Dziedziną funkcji homograficznej jest zbiór    natomiast zbioW

wartości jest R \{f-} -

Dowolną funkcję homograficzną można przedstawić w postaci /(x)=-^+0, gdzie p i q są współrzędnymi wektora przesunięcia wykresu funkcji postać y-\ dlaflj *0.

Wykresem dowolnej funkcji homografieznej jest hiperbola, którą możeaf uzyskać jako przesunięcie hiperboli o równaniu y-^ (por. ilustracje lx i 1.53) o wektor v = \p, q). Na poniższych rysunkach znajdują się wykresy funkcji y-^ oraz y = --7 - jako przykłady funkcji y =-^- odpowiednio dla a,>1 oraz tt, < 0.

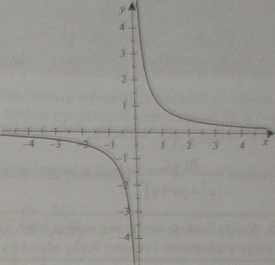
Ilustracja 1.52. Wykres funkcji y = —

Ilustracja 1.53'. Wykręć funkcji y s—-J*