P1080540 (3)

64

ściu obserwacji (j = 1,..., 6). Wyniki estymacji parametrów strukturalnych poszczególnych modeli zestawiono w tab. 1.19.

Tabela 1.19

Wyniki estymacji parametrów strukturalnych

Kwartał	Równanie modelu	Współczynnik determinacji R^2	Standardowy błąd oceny modelu s
I	yj, -6,020 + 0,223^,	0,966	0,088
n	yj2 - 6,880 + 0,991tj2	0,991	0,052
m	9p =6,593+0,269ltj3	0,976	0,088
IV	9j4 - 7,040 + 0,274tj4	0,997	0,029

Źródło: obliczenia własne wykonane w arkuszu kalkulacyjnym Excel.

Parametry zestawione w tabeli świadczą o tym, że oszacowane funkcje trendu są dość dobrze dopasowane do danych empirycznych, na co wskazują stosunkowo małe standardowe błędy oceny modeli oraz bliskie jedności współczynniki determinacji. Oszacowane równania linii trendu dla poszczególnych faz cyklu dają wystarczającą podstawę do dokonywania krótkookresowych prognoz wielkości sprzedaży rękawic roboczych w kolejnych kwartałach 1998 r.

Na rys. 1.19 przedstawiono segmenty szeregu czasowego wyznaczone dla okresów jednoimiennych, czyli poszczególnych kwartałów lat 1992-1997.

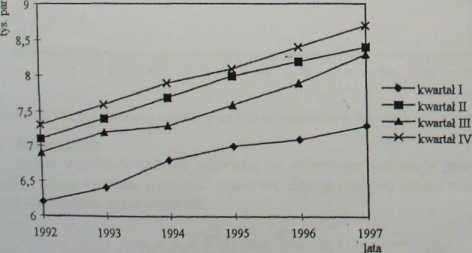
Rys. 1.19. Sprzedaż rękawic roboczych w okresach jednoimiennych

Korzystając z metody trendów jednoimiennych okresów i stosując regułę podstawową wyznaczamy prognozy wielkości sprzedaży na poszczególne kwartały kolejnego cyklu, czyli na rok t ^m k + 1 = 7. Prognozy zostaną wyznaczone przez ekstrapolacje oszacowanych linii trendu. W tab. 1.20 przedstawiono prognozowane wielkości sprzedaży dla kolejnych kwartałów 1998 r. oraz oceny dokładności tych prognoz w postaci bezwzględnego i względnego błędu prognoz ex antę.

Tabela 1.20

Prognozy i Wędy prognoz sprzedaży rękawic roboczych

Kwartały	Prognoza na rok 1998	Bezwzględny błąd tx ante v,	Względny błąd er ant* n, (w
I	y^j = 6,020 + 0,223 • 7 - 7,581	0,120	1,58
n	y]A = 6,880 + 0,263 • 7 - 8,721	0,071	0,t2
m	y V = 6,593 + 0,269 • 7 = 8,476	0,120	1.42
rv	yu = 7,040 + 0,274 • 7 = 8,958	0,040	0,45

Źródło: obliczenia własne wykonane w arkuszu kalkulacyjnym Excel.

Przewidywana wielkość sprzedaży rękawic roboczych w I kwartale 1998 r. wyniesie 7,6 tys. par, w II kwartale tego roku - 8,7 tys. par, w m kwartale - 8,5 tys. par, a w IV kwartale - 9,0 tys. par. Porównując otrzymane wartości względnych błędów ex antę z jego krytyczną wartością 4%, możemy uznać wyznaczone prognozy za dopuszczalne, wyznaczone błędy względne bowiem nie przekroczyły zadanej wartości krytycznej.

A Analiza harmoniczna

Zjawisko okresowości w szeregu czasowym można badać i prognozować również za pomocą analizy harmonicznej.

Analiza harmoniczna polega na budowie modelu w postaci sumy harmonik, czyli funkcji sinusoidalnych lub cosinusoidalnych o danych okresach. Pierwsza harmonika ma okres równy długości okresu badanego, druga -połowie tego okresu, trzecia - jednej trzeciej itd. W przypadku n obserwacji