str180 (3)

3. PRZEKSZTAŁCENIE LAPLACE’A I JEGO PEWNE ZASTOSOWANIA 180 § 3. WYZNACZANIE

Podstawiając wzory (5) i (6) do układu (3), otrzymujemy po przekształceniach

(S—l)LOO-L(_Z-> = - ‘

'    ^w S-1

L(y) + (S-l)L(z) = l.

Rozwiązując układ (7) względem niewiadomych L(y) oraz L(z), otrzymujemy

2    ...    (S—l)² —1

(8)

L(y) =

(S-l)² + l

L(z) =

Stosując do każdego równania układu (8) obustronnie przekształcenie odwrotne Laplace’a, otrzymujemy odpowiednio

^{(9)    l =2L} ((ś-i)²+i)’ ^{Z = L} ((s-i)²+i)^_l ((S—1) [(S—1)²+1])

Z tablicy przekształceń odczytujemy

(10)

L ¹ (--j = e⁽ sin t, L ¹ [ —-—^^ = e'

V(S-1)² + 1/    '    +

cos t.

Stosując twierdzenie o splocie (wzór 3.9), wyliczamy dalej, korzystając z (10), że

¹ ((S—1)[(S—1)²+1]) ^{= L}    ((s-i)² + i) ⁼

= (e')*(e'sint) = je^<'“^r)e^tsinTdr = —e'cost + e'.

Ostatecznie

(U)

((S-i

1

= e'(l— cost).

D[(s-i)²+a

Podstawiając wzory (10) i (11) do wzorów (9), mamy

y = 2e'sint, z = e'(2cost— 1).

Zadanie 5.13. Przez obydwa krańce cienkiego pręta o długości 2a dopływa stały strumień ciepła o gęstości q. Wyznaczyć przebieg zmian temperatury t{x) wzdłuż pręta znajdującego się w stanie ustalonym pod względem cieplnym, jeżeli jego powierzchnia boczna oddaje ciepło na zewnątrz według prawa Newtona.

Rozwiązanie. Przyjmujemy, że ł(x) dla —    jest przyrostem temperatury pręta

ponad stałą temperaturę otoczenia. W takim przypadku funkcja /(a) spełnia równanie różniczkowe

d²t

(1)

oraz następujące warunki brzegowe:

(2)

dt \    fdt\

<W*=o    °’    \ <**/*-« ^q’

gdzie

L — obwód przekroju poprze a — współczynnik przejmowa Transformujemy obecnie = «[/(a)]:

S²

stąd po uwzględnieniu warur

(3)

Funkcja T(S) ma dwa biegu Wyznaczamy obecnie orygim

2

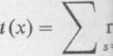
k=l

^,<0)[s

Dla wyznaczenia /(O) stosuje funkcji /(a) opisującej pole i

Zadanie 5.14. Funkcja x( spełnia równanie różniczkow

(1)

gdzie M — masa, n — wspć własnych do wychylenia, /(/) jeżeli w chwili t = 0 rozważ: