str036 (5)

36 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

1. istnieją w tym punkcie pochodne cząstkowe części rzeczywistej u{x,y) oraz urojonej v(x, y),

2. pochodne te spełniają w tym punkcie równania

dv

8x

(5.2)

du dv    du

°^raZ d~y ⁼

Równania (5.2) nazywamy równaniami Cauchy-Ricmanna.

Twierdzenie 2 (warunek dostateczny różniczkowalności). Jeżeli część rzeczywista u(x, y) oraz urojona v(x, y) funkcji zespolonej /(z) — u+iv spełniają równania Cauchy--Riemana w pewnym obszarze D i jeżeli nadto pochodne cząstkowe tych funkcji są ciągle w tym obszarze, to funkcja /(z) = u+iv ma w każdym punkcie z = x+iy tego obszaru pochodną:

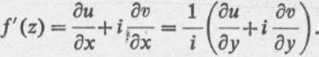
Definicja 2. Mówimy, że funkcja /(z) jest holomorficzna w punkcie z₀, jeżeli jest różnicz-kowalna w danym z₀ i w pewnym otoczeniu tego punktu.

Definicja 3. Mówimy, że funkcja /(z) jest holomorficzna w pewnym obszarze D, jeżeli jest holomorficzna w każdym punkcie tego obszaru.

Interpretacja    geometryczna    pochodnej.    Niech funkcja

(5.3)    w    =/(z)

będzie    holomorficzna    w    punkcie    z₀    oraz    niech f'(z₀)    # 0. Niech dalej

(5.4)    z    = z(t),

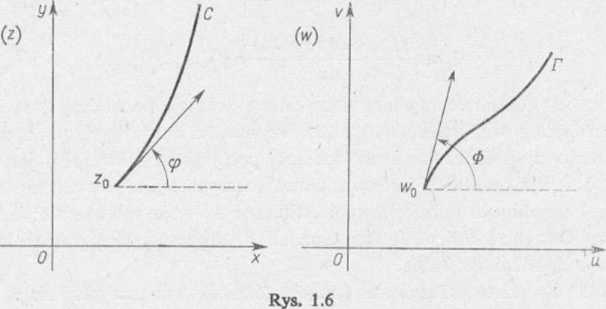
gdzie to^t^ti będzie równaniem łuku regularnego C, przechodzącego przez punkt z₀ = z(t₀). Łuk ten przy przekształceniu (5.3) przechodzi w krzywą f o równaniu

(5.5)

w=/[z(0] = vv(0,