str074 (5)

74 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

b) Bierzemy pod uwagę funkcję

(5)

R(z) =

1 + z⁴’

która dla rzeczywistych wartości z = x pokrywa się z funkcją podcałkową

1

oraz

9)    res,, R(z) = res.T-

(6)

*(*) =

l+.x^4>

Stwierdzamy teraz, źe funkcja R(x) spełnia założenia lematu 1. Zauważmy następnie, że funkcja R(z) określona wzorem (5) ma cztery bieguny, z których każdy jest jednokrotny. Bieguny te są miejscami zerowymi funkcji (ł + z⁴). W celu znalezienia tych miejsc zerowych rozwiązujemy równanie

(1 + z⁴) = 0,    z⁴ = -1.

Wiadomym sposobem wyznaczamy wszystkie pierwiastki czwartego stopnia z—1. Oto one

J2 J2

-o = cos£ir+ i sin    = -^—M —,

J2 J2

z_x = cos(i7t + J7t) + /sin(i7t+i7t) = ~2⁺*~2~ ’

J2 J2

z₂ = cos (i Tc + rc) + i sin Q jc + Jt) = —-—i- — ,

J2 J2

z 3 = cos (łrc+|it) + i sin(£n+ftc) = ~— i~~.

Z powyższych czterech liczb tylko z₀ oraz z_t są biegunami leżącymi w górnej półpłaszczyź-nie. Biorąc powyższe pod uwagę i stosując do funkcji R(x) wzór (10.5), mamy w rozważanym przypadku

+ oo

(7)

r dx

J ⁼ 2Ki

[res„₀ R(z)+res., R (z)]

Zgodnie ze wzorem (10.2') zastosowanym do R(z) kolejno w biegunach jednokrotnych z₀ i z₁ po uwzględnieniu wzoru Moivre’a mamy odpowiednio

, 1 1

res R (z) = res_zn--_z =-—

²ⁿ|_l + z⁴J (1 + z⁴)'

1

|i*zo ^4zO 1

4 (cos 4-71 + i sin in)³ 4 (cos |it + i sin |7t) 1    1 i

VL_;V2\ 4^/2 4^2

4 [COS (; 4[cos^

Podstawiając wzory (8) i (9) 1

+ 00

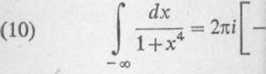
Zadanie 10.4. Obliczyć cal

+ 00

cos xdx ^ (,x² + l)(x² + 9)’

Rozwiązanie, a) Bierzer

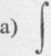
(1)

której część rzeczywista dla 1 całkową. Zauważmy teraz, ż Jordana. Stwierdzamy następ (2)    z, = i,

bieguny. Każdy z tych biegunc tylko dwa, a mianowicie z, 1 wyższe pod uwagę i stosując przypadku

+ 00

^<3)    1 (?7

-00

Zgodnie ze wzorem (10.2'), krotnych Zj oraz z₃, otrzyn

(4)    res_Zlf(z) = res_:

e

⁼ 4F

(5)    res_Z3/(z) = res,

(8)