Dziawgo; Działania na macierzach, podstawpwe typy macierzy 3

54 Działania na macierzach, podstawowe typy macierzy

Rozwiązanie:

x, 1

X'-I =

1

^xl	1'		X? +1	X, + x9		"1	0"
1		-1 =		1 l	—
1	X to 1_		Xj + x2	X2 +1 _		0	1

x,+x₂

_^xi	+ x2	^X2	-
' X?	x,+x2		a^2	-2 a
_x, + x2	^X2 .		_-2a	a^2

Przyrównując do macierzy A otrzymujemy:

Równe macierze mają te same elementy na odpowiednii li współrzędnych.

Zatem:

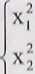
x, -I- x ₂ = -2a

Rozwiązujemy ten układ rów nań pamiętając, że

x²=a² <=> x^r=a v x=-a.

Ostatecznie, jedynym punktem spełniającym warunki naszego zadania jest punkt l’(-a,-a).

Zadanie 4.

Udowodnić, że macierze Grama G, = X-X^T, G₂ = X^T -X są macierzami symetrycznymi. Czy są to macierze równe?

Rozwiązanie:

Niech X_mxn.

q _ y

l mxn nxm    Działanie wykonalne. Macic)

_T    T    G! jest macierzą kwadratową

G[=(x-X^T) =(X^T) X^T=X-X^T = G, Stopnia m.

Zatem macierz Gi jest macierzą symetryczną. Analogiczne można pokazać, że macierz G2 jest symetryczna.

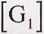
mxm

G₂ = XL_nX_mx„ => [0₂]„„

Widać, że macierze G|, G,> mogą hyć różnych wymiarów (jeśli tylko macierz N nie jest kwadratowa). Wiyc równośi miydzy nimi „na ogól” nie zachodzi

I)

U) A N I A .

• ln|i|c dane macierze:

1 -1 2“		"2	1	1 '		"0	-f
0 1 0	B=	1	2	1	, o	2	1
1 -1 3_		-1	-3 -1			_2 -3

1 -1

2 O

E=

1    1 O'

-1 1 -2

oblicz:

d) C(A+B), h) B+C².

.»)(■' i Li,    b) D³,    c) (A+B)^t-E^t,

• ) M 3B,    f)A²-C,    g)E-C,

' Uuji\c dane macierze:

					"0 r
	1 -1 0"		"2 1 -f
A	2 1 1	, B=	1 1 0	, c=	-1 2
					_ 1 1

oblicz AC+BC. Czy ten sam wynik można uzyskać wykonując tylko jedno mnożenie macierzy? t Wykonaj działania:

a)

!>)

cos a	-sma
sin a	cos a
cosx	sin x
sin x	cosx

cosb -sinb sin b cos b

t < l/nsndnij na podstawie definicji, że następujące macierze są idempotent-

no.

a)

1	A		'1	r
4	4	, b)	2	2
	3		1	1
„ 4	4 .		_2	2_

> c)

2

-4i -i