skanuj0085

166 5. Równowagi jonowe w rozcloricaonych roztworach woduych

Stała protolizy kwasu mrówkowego pK_a=3,75; stała protolizy kwasu octowego pK*“ 4,76; iloczyn jonowy wody pKw *=14.    '^;

166 5. Równowagi jonowe w rozcloricaonych roztworach woduych

CZĘŚĆ A

Przed dodaniem kwasu woda ma odczyn obojętny (równanie (11)).

₄_7 mol dm³

pH"- logc

H»0*

7,00

00.1)

(10.2)

Po dodaniu 1 mola kwasu HCI do 10 dm³ wody otrzymuje się roztwór kwasu solnego o stężeniu c = 0,1 mol/dm³. Wartość pH tego roztworu można obliczyć zgodnie ze wzorem (1.13):

pH = - log c = 1,00    (103)

CZĘŚĆ B

Jak obliczono w przykładzie 2, wartość pH roztworu kwasu mrówkowego o stężeniu formalnym C| = 1,0* 10^-3 mol/dm³ wynosi:

pH-3,47    (10.4)

Po dodaniu kwasu HCI otrzymuje się .roztwór stanowiący mieszaninę kwasu mrówkowego o stężeniu formalnym c, - 1,0-10"³ mol/dm³ i kwasu solnego ó stężeniu toitnainym Cs “ 0,1 móPdm^T '

MODEL STECHJOMETRYCZNY

HCOOH + H₂0 * HCOO" + HjO⁺    (10.5)

HCI + H₂0 -► C1-+H₃0⁺    (10.6)

2H₂0 ss HjO⁺ + OH"    (10.7)

Składniki roztworu: jony HjO^HCOO', Cl^OH" i cząsteczki HCOOH i H₂0.

MODEL MATEMATYCZNY Opis równowagi

_K,.w-y    ₍₁₀₈₎

^CHCOOH

^K»^=C._łj0*'^C0H-    i®

..............

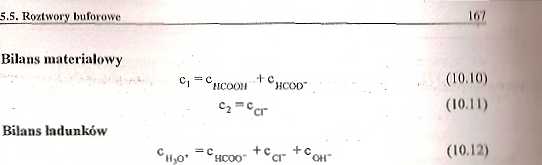
Ocena kompletności modelu matematycznego

Model składa się z pięciu niezależnych liniowo równań (10.8) - (10.12)_a które wiążą nieznane wartości stężeń c_Hj0., c_cr , c_HC0Q_, c_0|r , c_lłC00„ ,_A

Przyjęto, że stężenie wody jest stałe i wynosi c_Hj0 - 55,34 mol/dm³. Równanie definicyjne pH stanowi uzupełnienie modelu. Model jest kompletny.

UPROSZCZONY MODEL MATEMATYCZNY Uproszczenie modela

Podobnie jak w przykładzie 2 rozwiązanie modelu poprzez analizę matematyczną prowadzi do równania trzeciego stopnia. Model można uprościć. W roztworze tych dwóch kwasów musi być spełniona zależność:

So*^>>coh- ^>20    *(10.13)

--------------------------------------_______^

iw równaniu (10.12) można pominąć stężenie jonów wodorotlenkowych.

Rozwiązanie

Równanie (10.12) można teraz zapisać:

im.    <^i(u4)

Ponieważ c_a__sę_2l więc:

^CHCOO-^=C„^-^C2    <^l015)

Z równania (10.10) oblicza się stężenie kwasu mrówkowego:

°hcooh =C| ~^chcoo- “Cl +Oj -C_M)0.    (10.16)

Podstawiając (10.15) i (10.16) do wyrażenia na stałą K_a (10.8) otrzymuje się równanie: