Untitled 28

126

j. rrzyonzone rozwiązywanie równań nieliniowych i ich układów

3

x, = 2--(2- 1) = 1,57142

*2 = ² - . J.-.C2 - 1,57142) = 1,70540 4,36449

itd.

Jak widać, w metodzie siecznych znacznie szybciej niż w metodzie reguła falsi otrzymujemy wynik przy tej samej zadanej dokładności. Zbieżność metody reguła falsi w porównaniu z metodą siecznych jest znacznie wolniejsza w pobliżu pierwiastka.

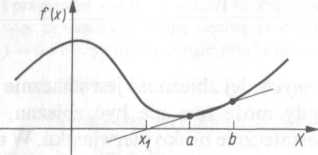
Przy stosowaniu metody siecznych jest niezbędne, aby pierwsza iteracja zaczynała się z punktów, w których funkcja ma różne znaki, w przeciwnym razie możemy wykryć nieistniejący pierwiastek (rys. 3.5), co jest szczególnie niebezpieczne przy obliczeniach prowadzonych na maszynach cyfrowych.

Ćwiczenia

1.    Omówić metodę reguła falsi i ocenę błędu.

2.    Jaka jest różnica pomiędzy metodą reguła falsi a metodą siecznych?

3.    Obliczyć metodą reguła falsi przybliżony pierwiastek równania sinx + x — 1 = 0

położony między a = 0 i b ■

1. Obliczenia zakończyć, gdy |sin x* + x* — 11 < - • 10^-2.

4.    Rozwiązać przykłady podane w ćwicz. 7, p. 3.1.1 stosując metodę reguła falsi.

5.    Obliczyć metodą siecznych pierwiastek równania e^x — 3x² = 0 położony w pobliżu punktu x₀ = —0,5.

6.    Znaleźć miejsce zerowe funkcji y — 3x + sin x — e^x w przedziale <0; 1) za pomocą metody siecznych.

7.    Napisać schemat blokowy programu do obliczania przybliżonej wartości pierwiastka równania 2x⁴ — 5x² + x + 1 = 0 z zadaną dokładnością e.

Odpowiedzi. 3. 0,5110. 5. x = -0,458962. 6. x = 0,3604.

ł.1.3. Metoda Newtona. Metody zmodyfikowane dla pierwiastków wielokrotnych

Przybliżoną wartość pierwiastka równania (3.1) przy założeniu, że na przedziale <a; b>, w którym położony jest pierwiastek, funkcja f(x) ma w końcach różne znaki oraz pierwsza i druga pochodna mają stały znak, można wyznaczyć też metodą Newtona, zwaną także metodą stycznych. W metodzie tej z tego końca przedziału <a; ó>, w którym funkcja f(x) ma ten

3.1 ■ Jedno równanie z jedną niewiadomą

127

sam znak co f"(x) prowadzimy styczną do wykresu funkcji y =f(x) i punkt x_u w którym ta styczna przecina oś OX przyjmujemy za pierwsze przybliżenie szukanego pierwiastka a. Oczywiście/(jc,) ma ten sam znak co rzędna punktu, z którego wyprowadzona była styczna. Jeżeli otrzymane przybliżenie jest za mało dokładne, to z punktu o współrzędnych (*,, /(*,)) prowadzimy następną styczną. Punkt x₂ przecięcia tej stycznej z osią OX jest drugim przybliżeniem pierwiastka. W ten sposób otrzymujemy kolejne wyrazy ciągu przybliżeń

x_u x₂, ..., x_n, ...

zbieżnego monotonicznie do a [17].

Na rysunku 3.6 pokazano geometryczną interpretację metody Newtona dla przypadku, gdy zarówno pierwsza, jak i druga pochodna funkcji f(x) są

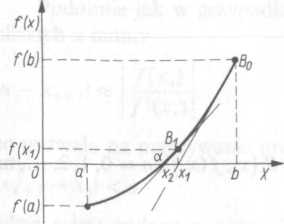
dodatnie na rozpatrywanym przedziale. Styczną prowadzimy z punktu B₀ (bowiem f'{b) > 0 i f"(b — )> 0). Jej równanie ma postać

y ~f(b) =f'(b)(x - b)

Przyjmując y = 0, otrzymamy

=_b-m

f\b)

(3.14)

Wykażemy, że jci leży bliżej a niż b. Korzystając ze wzoru Taylora mamy

/(a) =f(b) +/'(&)(« -b) + \f"{c)(* - b)² gdzie ce(a; b). Ponieważ/(a) = 0, więc

f'(b)    2f(b)    ¹

i wobec (3.14)

(3.15)

2 f'(b)

(a - b)² < 0