Ćwiczenie O-2 |
Grupa 12b WYDZIAŁ MECHANICZNY |
|
Temat: Wyznaczanie skręcenia właściwego roztworu cukru.
Skręcenie płaszczyzny polaryzacji
|
Data |
Ocena |
Podpis |
Teoria |
|
|
|
Wykonanie |
|
|
|
Sprawozdanie
Celem naszego doświadczenia jest wyznaczenie kąta skręcenia płaszczyzny polaryzacji oraz wyznaczenie kąta skręcenia właściwego roztworu cukru. Do tego celu użyliśmy: polarymetr, komplet badanych roztworów cukru, woda destylowana.
Wstęp
Teoria elektromagnetyczna mówi, że światło, podobnie jak każde promieniowanie
elektromagnetyczne jest falą poprzeczną.
Teoria
Polaryzacją światła nazywamy sprowadzenie drgań poprzecznej fali świetlnej do jednej
płaszczyzny. Płaszczyzną polaryzacji (płaszczyzną drgań) jest płaszczyzna, którą wyznaczają przy polaryzacji liniowej wektor świetlny E i kierunek promienia r. Natomiast polaryzacja kołowa polega na tym, że wektor E obraca się wokół promienia jako osi obrotu.
W normalnych warunkach polaryzacja światła zachodzi podczas odbicia od przezroczystych dielektryków (woda,szkło) oraz podczas rozpraszania światła (światło słoneczne w atmosferze). Falę spolaryzowaną można wytworzyć za pomocą polaryzatora.
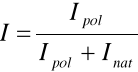
Fala niespolaryzowana jest to fala, w której kierunek pola elektrycznego jest prostopadły do kierunku rozchodzenia się fali. Wiązka światła niespolaryzowana polaryzuje się częściowo przy odbiciu lub załamaniu w środku izotropowym. Stopień polaryzacji wiązki światła, gdy natężenie fali świetlnej w wiązce jest I, to część energii przypada na światło całkowicie spolaryzowane Ipol, pozostała część na niespolaryzowane Inat to stopień polaryzacji wynosi:
Natężenie fali całkowicie spolaryzowanej po przejściu przez analizator zmienia się zgodnie z prawem Maluza:
I = I0 ⋅ cos2α
Współczynnik załamania światła równa się tangensowi kąta padania α tzn, gdy promień odbity i załamany tworzą ze sobą 900, wówczas cały promień odbity jest całkowicie spolaryzowany.
Skręcenie właściwe k dla roztworów jest równe liczbowo wartości kąta skręcenia płaszczyzny polaryzacji po przejściu przy jednostkowym stężeniu (zwykle 1g/ml).
Skręcenie właściwe zależy od temperatury i od długości fali świetlnej λ.
Zdolność skręcania płaszczyzny polaryzacji wykazują bardzo liczne związki organiczne oraz ich roztwory w cieczach skręcających np. roztwory cukrów, białek, kwasów organicznych.
Kąt wygląda wtedy:
α = k ⋅ c ⋅ l
gdzie : k - skręcenie właściwe danej substancji s
l - długość drogi światła w roztworze
Kąt skręcenia α zależy od rodzaju substancji i długości fali użytego światła oraz od stężenia (roztwory) oraz od grubości warstwy skręcającej l.
W celu wyznaczenia właściwego skręcenia płaszczyzny polaryzacji użyliśmy polarymetru.
Polarymetr jest to przyrząd służący do pomiaru kąta skręcenia płaszczyzny polaryzacji. Działanie przyrządu oparte jest na wykorzystaniu właściwości oka, które z dużą dokładnością może ocenić, czy jasność dwu sąsiadujących ze sobą pól jest jednakowa. Podstawową częścią polarymetru jest płytka kwarcowa - polaryzator oraz analizator połączony z podziałką kątową. Płaszczyzna polaryzacji wiązek przechodzących przez boczne części płytki jest skręcone w stosunku do płaszczyzny polaryzacji wiązki przechodzącej przez część ośrodkową o tzw. kąt położenia.
Między polaryzatorem a analizatorem umieszczamy rurkę z roztworem. Pomiarów dokonuje się w świetle monochromatycznym z zastosowaniem lampy sodowej lub odpowiedniego filtru optycznego.
Znając długość l rurki z cieczą oraz skręcenie właściwe k substancji liczymy ze wzoru
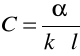
Przyrząd do badania stężeń cukru nosi nazwę sacharymetru. Ma zastosowanie w badaniu zawartości glukozy u chorych na cukrzycę.
Obliczenia
Rozkład wyników pomiarów uzyskany dla skończonych prób, zwany jest rozkładem
Studenta-Fischera. Dla małych prób, wartości Sx różnią się znacznie od parametru rozkładu normalnego σ. Teoria Studenta-Fischera dowodzi, że obliczone wartości Sx należy pomnożyć przez odpowiednie poprawki, tzw współczynniki studenta tnα
|
1% |
2% |
3% |
4% |
5% |
Cx |
X1 |
1 |
2.5 |
3.3 |
3.9 |
6.9 |
1.4 |
X2 |
1.3 |
2.2 |
3.5 |
4.5 |
7.1 |
1.6 |
X3 |
1.4 |
2.4 |
3.6 |
4.4 |
7 |
1.8 |
X4 |
1.7 |
2.2 |
3.8 |
4.5 |
7.2 |
2.2 |
X5 |
1.8 |
2.4 |
4 |
4.2 |
7.1 |
2.1 |
X = αśr - średnia wartość
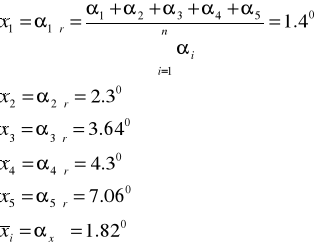
Woda destylowana:
|
1 |
2 |
3 |
4 |
5 |
Kąt |
00 |
0.10 |
00 |
0.20 |
0.10 |
Przyjmujemy poziom ufności 0.9
Dla 5 pomiarów tnα = 2.13 t∞α = 1.64
ωt = wielkość względnego błędu systematycznego
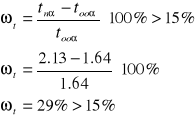
Wykorzystujemy odchylenie standardowe pojedynczego pomiaru po uwzględnieniu poprawek Studenta-Fischera
σ = tnα Sx tnα = 2.13 dla poziomu ufności = 0.9
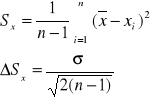
n - liczba pomiarów
- odchylenie standardowe
Obliczamy błędy wszystkich pomiarów każdego roztworu :
|
1% |
2% |
3% |
4% |
5% |
Sx1 |
0.04 |
0.01 |
0.03 |
0.04 |
0.0064 |
σ1 |
0.085 |
0.0213 |
0.06 |
0.08 |
0.012 |
Δ Sx1 |
0.03 |
0.007 |
0.02 |
0.03 |
0.004 |
Sx2 |
0.0025 |
0.0025 |
0.005 |
0.01 |
0.0004 |
σ2 |
0.005 |
0.0054 |
0.01 |
0.02 |
0.00085 |
Δ Sx2 |
0.002 |
0.002 |
0.003 |
0.007 |
0.0003 |
Sx3 |
0.0025 |
0.0025 |
0.0004 |
0.002 |
0.0009 |
σ3 |
0.005 |
0.0054 |
0.0008 |
0.004 |
0.002 |
Δ Sx3 |
0.002 |
0.002 |
0.0003 |
0.001 |
0.0007 |
Sx4 |
0.0225 |
0.0025 |
0.006 |
0.01 |
0.005 |
σ4 |
0.048 |
0.0054 |
0.01 |
0.021 |
0.011 |
Δ Sx4 |
0.02 |
0.002 |
0.003 |
0.007 |
0.004 |
Sx5 |
0.04 |
0.0025 |
0.03 |
0.002 |
0.0004 |
σ5 |
0.085 |
0.0054 |
0.06 |
0.004 |
0.00085 |
Δ Sx5 |
0.03 |
0.0002 |
0.02 |
0.001 |
0.0003 |
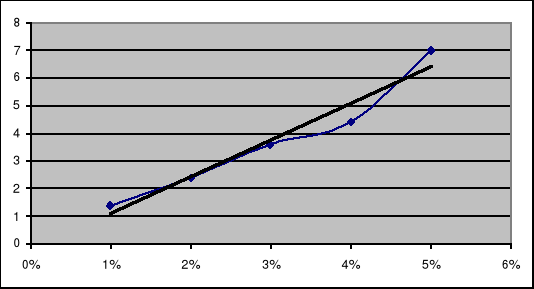
Wykonujemy wykres zależności kąta skręcenia płaszczyzny polaryzacji i stężenia roztworu cukru (C[%]) metodą regresji liniowej
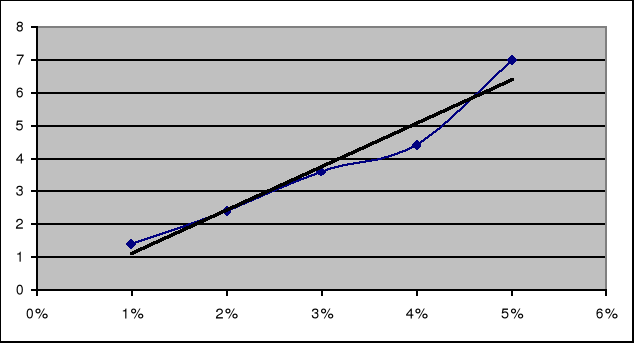
Wartość Cx odczytujemy z wykresu
Cx = 1.3 %
4.Wniosek
Stwierdziliśmy, że wraz ze wzrostem stężenia roztworu cukru wzrasta kąt skręcenia płaszczyzny polaryzacji.
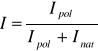
![]()
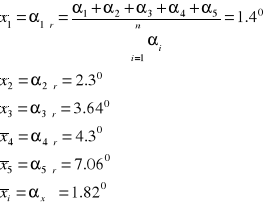
![]()
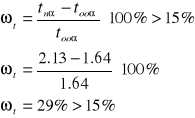
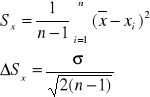
Wyszukiwarka
Podobne podstrony:
02, laborki O2 - jaiczeski, ĆWICZENIE 02
Ćwiczenie O2 doc
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
cwiczenia 9 kryzys
Ćwiczenia 1, cz 1
Ćwiczenie 8
9 ćwiczenie 2014
Cwiczenie 1
Ćwiczenie 2 Polska w europejskim systemie bezpieczeństwa
więcej podobnych podstron