Fizyka |
|
Rok akademicki |
Data |
|
Techniczna |
|
1998/99 |
23.10.1998 |
|
|
Sobczak Wojciech |
Semestr 1 |
|
|
|
|
|
Ocena |
Podpis |
Gr. 7 |
|
Ćw. 36 |
|
|
Mikroskop
Zasada Fermata wyraża się w następujący sposób : Promień świetlny biegnący z jednego punktu do drugiego przebywa drogę, na której przebycie trzeba zużyć w porównaniu z innymi, sąsiednimi drogami, minimum albo maksimum czasu, albo tę samą ilość czasu (w przypadku stacjonarnym.
Budowa mikroskopu
Mikroskop składa się z masywnego statywu podtrzymującego stolik i z części optycznych przyrządu. Obiektyw i okular są układami soczewek: obiektyw 2-10 sztuk, o średnicy paru mm i bardzo krótkiej ogniskowej, okular zazwyczaj z 2 sztuk o większej średnicy i dłuższej ogniskowej. Na rysunku przedstawiono bieg promieni w mikroskopie w którym okular i obiektyw są zastąpione pojedynczymi soczewkami. Oglądany przedmiot umieszczamy tuz za ogniskiem F1. Obiektyw wytwarza obraz A2B2 rzeczywisty, powiększony, odwrócony. Obraz ten służy jako przedmiot dla okularu, tez z kolei daje obraz A3B3 urojony prosty, powiększony. Zatem możemy powiedzieć że powiększenie mikroskopu jest to stosunek wymiarów liniowych obrazu do odpowiednich wymiarów liniowych przedmiotu ![]()
widać więc że powiększenie mikroskopu jest iloczynem powiększenia ![]()
(powiększenie obiektywowe) i powiększenia ![]()
(powiększenie okularowe). Z rysunku możemy odczytać że : ![]()
i ![]()
gdzie l jest długością tubusu mikroskopu a D odległością dobrego widzenia (ok. 25 cm) stąd otrzymujemy : ![]()
Dodać można jeszcze że mikroskopy wyposażane są w kilka wymiennych obiektywów i okularów.
Pomiar powiększenia obiektywu.
Aby wyznaczyć powiększenie okularu należy ustawić mikroskop na ostry obraz skali dzielonej na 0,1 mm, zdjąć okular i zastąpić go matową szybką. Widać wtedy na szybce rzeczywisty, powiększony, odwrócony obraz skali. Należy teraz przyłożyć do tego podziałkę milimetrową i policzyć ilość mm (a) oglądanych wprost przypadającą na pewną ilość (b) dziesiętnych części mm obrazu na matówce. Powiększenie sprawione przez obiektyw możemy teraz obliczyć korzystając ze wzoru:
![]()
![]()
W przypadku naszego ćwiczenia wyznaczaliśmy powiększenie obiektywu korzystając z dwóch skal obserwowanych przez obiektyw 0,1 mm oraz 0,01 mm
Otrzymane wyniki pomiaru zestawiono w tabeli:
Dla obiektywu 40x i podziałki 0,01 mm
a- [dz] |
b- [dz] |
8,5 |
20 |
8,5 |
20 |
8,5 |
20 |
--------------------------------------------- |
---------------------------------------------- |
17 |
40 |
17 |
40 |
17 |
40 |
Korzystając ze wzoru obliczam : ![]()
= 42,5x i
![]()
= 42,5x
obliczam błąd
![]()
![]()
stąd mam że : ![]()
czyli : ![]()
więc otrzymuję że ![]()
te same obliczenia wykonuję dla drugiego pomiaru i otrzymuję że:
![]()
![]()
, ![]()
i wynik ostateczny ![]()
Dla obiektywu 10x i podziałki 0,1 mm
a- [dz] |
b- [dz] |
11 |
10 |
11 |
10 |
11 |
10 |
--------------------------------------------- |
---------------------------------------------- |
13 |
12 |
13 |
12 |
13 |
12 |
![]()
= 11x i
![]()
= 10,8x
stąd ![]()
oraz ![]()
![]()
![]()
![]()
we wszystkich przypadkach wyniki pomiarów zmieściły się w granicy wyznaczonego błędu co oznacza ze wszystkie pomiary są prawidłowe.
Pomiar średnicy kapilary
Do pomiaru średnicy kapilary wykorzystano okular mikrometryczny, jest to nic innego jak zwykły okular Huygens'a zaopatrzony w skalę. Okular taki składa się z dwóch soczewek płasko-wypukłych o różnych ogniskowych. Umieszcza się go w takiej odległości od obiektywu, aby obraz rzeczywisty przedmiotu wytworzony przez obiektyw wypadł pomiędzy soczewkami. Podziałkę milimetrową (0,01mm) umieszczamy na statywie i staramy się uzyskać możliwie jak najostrzejszy obraz oglądanej podziałki. Następnie należy obliczyć na ile działek skali obiektywowej przypadają działki skali okularowej, a następnie z prostej proporcji obliczyć jakiej długości odpowiada jedna „kreska” skali okularowej. Na tak wywzorcowanym mikroskopie możemy przejść do pomiaru średnicy kapilary.
W tym celu należy na uprzednio wywzorcowanym mikroskopie uzyskać ostry obraz oglądanej kapilary, oraz zmierzyć jej średnicę za pomocą podziałki na okularze milimetrowym. Następnie należy pomnożyć uzyskany wynik przez wartość jednej działki i otrzymamy średnicę kapilary.
W naszym przypadku pomiar wyglądał następująco:
![]()
Wynika z tego że x = 0,08 mm, średnica kapilary odczytana z okularu mikrometrycznego była równa 6,8 działki co daje nam K = 0,544 mm
W przypadku tego pomiaru nie jesteśmy w stanie dowiedzieć się czy pomiar nasz był prawidłowy ponieważ nie mamy ani wartości tablicowej szerokości kapilary, ani nie została ona podana przez producenta próbki przeznaczonej do badania. Można jedynie podać błąd niepewności systematycznej pomiaru wynikającej z niedokładności przyrządu pomiarowego (w naszym przypadku podziałki 0,01 mm na wzorcu)
Stąd też możemy zapisać że średnica kapilary jest równa :
![]()
[mm]
Pomiar współczynnika załamania światła.
Współczynnikiem załamania „n” przy przejściu światła z ośrodka I do ośrodka II nazywamy stosunek sinusa kąta padania α do sinusa kąta załamania β ![]()
Zazwyczaj jako ośrodek I przyjmuje się powietrze. Gdy światło przechodzi z ośrodka „optycznie gęstszego” do powietrza to ![]()
. Metoda wyznaczania współczynnika załamania światła za pomocą mikroskopu wykorzystuje zjawisko przesunięcia obrazu punktu świecącego, sprawionego przez płytkę płasko-równoległą. (patrz rysunek)
Kładziemy na stoliku mikroskopu płytkę płasko równoległą z materiału przeźroczystego (szkło) z nakreślonymi atramentem znaczkami na górnej i dolnej powierzchni. Promienie wysłane przez punkt O na dolnej powierzchni płytki po przejściu przez powierzchnię górną ulegną załamaniu, przedłużenia ich przetną się w punkcie O, który dla obiektywu będzie odgrywał rolę przedmiotu. Odległość obu znaczków na płytce, równa grubości płytki d, oglądana przez płytkę i mikroskop wynosi d' = O'O”
Z rysunku możemy odczytać:
![]()
i jeżeli teraz założymy że kąt padania jest mały otrzymamy: ![]()
skąd
![]()
Grubość d wyznaczamy jako średnią z 10 starannie przeprowadzonych pomiarów za pomocą śruby mikrometrycznej, wyniki zestawiono w tabeli:
d- z pomiaru |
Δd |
(Δd)2 |
0,98 |
0,008 |
0,000064 |
0,96 |
0,0012 |
0,000144 |
0,98 |
0,008 |
0,000064 |
0,98 |
0,008 |
0,000064 |
0,96 |
0,0012 |
0,000144 |
0,98 |
0,008 |
0,000064 |
0,98 |
0,008 |
0,000064 |
0,96 |
0,0012 |
0,000144 |
0,96 |
0,0012 |
0,000144 |
0,98 |
0,008 |
0,000064 |
Średnia arytmetyczna S = 0,972
Odchylenie standardowe :
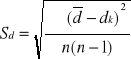
![]()
d = (0,927 ± 0,003) mm
błąd maksymalny wynosi :
Δdmax = 3Sd = 0,009
z czego otrzymujemy
d = (0,972 ± 0,009) mm
d' wyznaczamy za pomocą mikroskopu zaopatrzonego we wzorcowaną śrubę pozwalającą na drobne pionowe przesunięcia tubusu.
W naszym przypadku jedna działka na tej śrubie była równa 0,002 mm
Ostry obraz otrzymano po obrocie o 320 działek co po przemnożeniu daje nam wynik
d' = 0,64 mm
d' = (0,640 ± 0,002) mm
następnie obliczam współczynnik załamania światła korzystając ze wzoru :
![]()
![]()
maksymalny błąd bezwzględny wynosi
(Δn)max = n * 0,012 = 0,011
n = (1,518 ± 0,011)
ntab = 1,515
co utwierdza nas w przekonaniu ze ćwiczenie i pomiary zostały wykonane poprawnie.
Podsumowanie
W ćwiczeniu należy zwrócić szczególną uwagę na stosowany obiektyw oraz okular w przypadku pomiarów średnicy kapilary, oraz współczynnika załamania światła, wynika to z tego iż przy zastosowaniu za dużego powiększenia może okazać się niemożliwe odnalezienie badanego przedmiotu (kapilary, nadruku), lub też niemożliwe stanie się odczytanie na matowej szybce ilości działek na wzorcu (przy wzorcowaniu obiektywu). Należy także zadbać o czystość obiektywów i okularów gdyż zabrudzenia w znacznym stopniu mogą utrudnić pracę (niemożliwe jest wtedy dobre ustawienie ostrości oglądanego preparatu). Uwaga w przypadku stosowania obiektywu 10x należy w jednym z mikroskopów uprzednio wykręcić obiektyw 40X gdyż jego długość skutecznie uniemożliwia zbliżenie stolika z preparatem, tak aby ustawić ostrość.
O
O'
A3
B3
A2 B2
F2
F1'
A1 B1
Z
K
obiektyw
okular
Ilość działek na wzorcu
Wzorzec
Ilość działek na okularze
II
I
β
α
d'
O
O'
O”
α
A
α
β
d
Wyszukiwarka
Podobne podstrony:
cw 13 fizyka
ćw.14, Fizyka, Skrypt do Laborek
ćw.27, Fizyka, Skrypt do Laborek
ćw.24, Fizyka, Skrypt do Laborek
ćw.31, Fizyka, Skrypt do Laborek
Elektroliza ćw. 2 i 5, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
ćw.20, Fizyka, Skrypt do Laborek
ćw.15, Fizyka, Skrypt do Laborek
cw 23 fizyka id 100377 Nieznany
cw-72-a, Fizyka laboratorium, Sprawozdania
cw 81, fizyka(1)
Cw 46, Fizyka Sprawozdania, Ćw nr 46, Ćwiczenie 46
ćw.12, Fizyka, Skrypt do Laborek
ćw.26, Fizyka, Skrypt do Laborek
ćw.23, Fizyka, Skrypt do Laborek
ćw.25, Fizyka, Skrypt do Laborek
ćw.13, Fizyka, Skrypt do Laborek
ćw.17, Fizyka, Skrypt do Laborek
więcej podobnych podstron