Sarlińska Agnieszka 172962 dr A. Kolarz
WPPT Inżynieria Biomedyczna II Sem. wt. 8:30
Ćwiczenia 81: Wyznaczanie promieni krzywizny soczewki i długości fali świetlnej za pomocą pierścieni Newtona
Cel ćwiczenia:
Zapoznanie się ze zjawiskiem interferencji światła występującym w klinie optycznym
Zastosowanie interferencji światła do celów pomiarowych
Wstęp teoretyczny:
Gdy wiązka światła pada na powierzchnię rozgraniczającą dwa różne ośrodki (różniące się współczynnikami załamania) , wówczas część światła odbija się, pozostała część przejdzie do drugiego ośrodka. Jeżeli dwie takie powierzchnie tworzą klin, to wiązki odbite od tych powierzchni, jako pochodzące od tego samego źródła (spójne), wzajemnie ze sobą interferują. Przykładem takiego klinu jest powietrzny klin interferencyjny, utworzony między dwoma wewnętrznymi powierzchniami płaskorównoległych płytek szklanych. We wszystkich punktach powierzchni dochodzi do nałożenia się obu fal odbitych. Amplituda zintegrowanej fali w A zależy od różnicy faz obu promieni, a więc od różnicy ich dróg optycznych Δ.
Zakładając, że kąt klina jest bardzo mały, a równoległa wiązka światła monochromatycznego pada na powierzchnię klina prostopadle, możemy obliczyć różnicę dróg optycznych między interferującymi promieniami. Oznaczając mianowicie grubość klina w danym miejscu przez h1,otrzymamy:
do geometrycznej różnicy dróg optycznych dodaje się dodatkową różnicę spowodowaną skokiem fazy o π podczas odbicia fali świetlnej na granicy powietrze- szkło, tj. od granicy ośrodka optycznie gęstszego. W tych miejscach klina, w których
nastąpi na skutek interferencji wygaszenie światła. Tam natomiast, gdzie
nastąpi interferencyjne wzmocnienie światła. W klinie, którego obie powierzchnie są płaskie, zaobserwujemy więc kolejno na przemian jasne i ciemne prążki. Każdy prążek jest miejscem geometrycznym równo odległych punktów obu powierzchni klina i stąd nazwa „prążki równej grubości”.
Prążki interferencyjne równej grubości można najłatwiej zaobserwować umieszczając na płaskiej płytce szklanej wypukło- sferyczną soczewkę. Tworzy się wówczas między powierzchnią płytki a powierzchnią soczewki klin powietrzny o zmiennym kącie. Prążki interferencyjne powstające w takim klinie- tzw. prążki Newtona- będą miały kształt kolisty. W miarę wzrostu odległości od środkowego ciemnego (zerowego) prążka, utworzonego w miejscu styku obu powierzchni, kolejne prążki coraz bardziej się zagęszczają, aż przestaną być w ogóle zauważalne. Podczas obserwacji wzrokowej powstawanie prążków Newtona można przedstawić wykreślnie.
Prążki Newtona wykorzystamy do obliczenia promienia krzywizny R soczewki. Należy w tym celu zmierzyć promień rk dowolnego k- tego ciemnego prążka oraz znać długość fali λ użytego światła.
Promień krzywizny obliczamy ze wzoru na promień R czaszy sferycznej o promieniu podstawy rk i wysokości czaszy hk:
Dla dużych wartości R, ponieważ r >> h, powyższy wzór można wyrazić w następujący sposób:
Wysokość czaszy hk, odpowiadającą k- temu prążkowi, można wyrazić
Wstawiając do wyrażenia na R otrzymujemy:
Wykorzystane wzory:
Przyjęte oznaczenia:
akp, akl - wskazania czujnika mikroskopu dla k- tego prążka;
λ- długość fali świetlnej;
k- numer prążka;
rk- promień k- tego prążka;
R- promień krzywizny soczewki;
Promień krzywizny soczewki wyraża się wzorem:
Średnicę k- tego prążka obliczamy na podstawie różnicy wskazań akp i akl czujnika mikroskopu. Promień rk k- tego promienia prążka można obliczyć na podstawie wzoru:
Długość fali świetlnej obliczamy na podstawie wzoru na promień krzywizny soczewki R:
Do wyznaczenia wartości średnich wskazań czujnika mikroskopu ap, al., promienia krzywizny R soczewki wykorzystujemy następujące charakterystyki liczbowe:
x - wielkość mierzona;
n- liczba pomiarów;
Niepewności pomiarowe liczymy za pomocą wzoru:
Wyniki pomiarów i przykładowe obliczenia:
Wyznaczanie promienia krzywizny soczewki:
\
Filtr IF 600
k |
al. [mm] |
ap [mm] |
r [mm] |
R [mm] |
1 |
8,29 |
8,35 |
0,03 |
0,54 |
2 |
8,34 |
8,46 |
0,06 |
1,08 |
3 |
8,22 |
8,56 |
0,17 |
5,78 |
4 |
8,13 |
8,65 |
0,26 |
10,14 |
5 |
8,03 |
8,74 |
0,355 |
15,123 |
6 |
7,94 |
8,86 |
0,46 |
21,16 |
średnia |
8,16 ± 0,15 |
8,6 ± 0,19 |
0,22 ± 0,17 |
8,97 ± 8,14 |
r1 = ![]()
[mm]
R1= ![]()
[mm]
RŚr = ![]()
[mm]
δRŚr= 8,14 = [mm]
RŚr = 8,97 ±8,14 [mm]
Filtr nieznany
k |
al. [mm] |
ap [mm] |
r [mm] |
λ [nm] |
1 |
8,31 |
8,53 |
0,11 |
1348,94 |
2 |
8,24 |
8,61 |
0,185 |
1907,75 |
3 |
8,12 |
8,7 |
0,29 |
3125,23 |
4 |
8,06 |
8,85 |
0,395 |
4348,52 |
5 |
7,92 |
8,92 |
0,5 |
5574,14 |
6 |
7,85 |
9,04 |
0,595 |
6577,95 |
średnia |
8,08±0,19 |
8,78±0,19 |
0,35±0,19 |
3813,75±2059,51 |
λ1=![]()
λŚr=3813,75 [nm]
δλŚr = 2059,51 [nm]
λŚr = 3813,75 ± 2059,51 [nm]
Wnioski:
Wykorzystane w doświadczeniu przyrządy pomiarowe były niedokładne w porównaniu z wielkością obserwowanych obiektów. Możliwy był też niezbyt precyzyjny odczyt wskazań czujnika oraz ustawienie krzyża na środku danego prążka. Wszystkie te czynniki ujemnie wpływają na dokładność pomiarów mierzonych wielkości. Należy też zauważyć, iż występująca we wzorze na długość fali promień krzywizny soczewki był wcześniej zmierzony również z pewnym błędem.
![]()
![]()
![]()
Schemat powstawania i obraz prążków Newtona
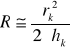
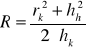
![]()
![]()
![]()
![]()
![]()
![]()
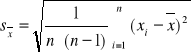
Wyszukiwarka
Podobne podstrony:
cw 81
cw 13 fizyka
ćw.14, Fizyka, Skrypt do Laborek
ćw.27, Fizyka, Skrypt do Laborek
ćw.24, Fizyka, Skrypt do Laborek
ćw.31, Fizyka, Skrypt do Laborek
ćw 81
Elektroliza ćw. 2 i 5, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
ćw.20, Fizyka, Skrypt do Laborek
ćw.15, Fizyka, Skrypt do Laborek
ćw.36, CW 36, Fizyka
cw 23 fizyka id 100377 Nieznany
cw-72-a, Fizyka laboratorium, Sprawozdania
Cw 46, Fizyka Sprawozdania, Ćw nr 46, Ćwiczenie 46
ćw.12, Fizyka, Skrypt do Laborek
ćw.26, Fizyka, Skrypt do Laborek
ćw.23, Fizyka, Skrypt do Laborek
ćw.25, Fizyka, Skrypt do Laborek
więcej podobnych podstron