04 (6)

Biblioteczka Opracowań Matematycznych

U

= 2 je’dx - J zLS—= 2 fe'dx - 2 Jx~^:dr

2x~‘    2

= 2e’    --h C = 2e' + — + C

— I    .x

8/    . _

— |*    4 cos 2x

3 cos ‘ x sin x

-dx

_ £ [-cos² x - sin ² x^ _ £ jcos² x-l + cos

cos² xsin² x

cos² xsin² x

-dx =

4 r 2 cos² X -1

3 ^J cos ‘ x sin * x

^x~^l _dx = 1 f 2cos² x ^ _ d_ j- dx _ 8 j- dx in ■ X 3 ■* COS ² X sin ² X 3 J cos ² r sin ¹ r 3 J cin ²

dx

8 r dx

3 ^J cos² x sin² x 3 ^J sin ‘ x

4 rcos* x + sin x

-tJ

cos xsin x

i x,    8    ł r cos x . ą r

2—ax = --ctgx ---—r—dx--

X    3    3 J ma ² r sin ² r 3 J

sin² x

3 ² cos² x sin² x 3 ^J cos² x sin² x

■dx

8___ 4 f dx 4 f dx    8    4    4

- - ~^C,S^X    ~ — I    ~—5--zr -;— =    - —crgx    + —ctgt--igx + C =

3    3 ^J    sin ²    x ?    ^! r x

=—Ctgx--lgx+C

r 1 — sin² jc sin² x

dx

sin².v

a/ f , 2 . rCOS‘x, rl-sm x , r dx r ,    „

9/ \ctgxdx=\ dx= ——-dx= [—--\dx = -ctgx-x + C

¹    J Sin X ^J sin² r    J sin² v J

10/ f-

- J Cl

lOfitc

sin² xcos² x

= 10 f—r-f ^{+ C}°f    = 10 f-

^J sin “ rrnę‘ v    J ci

sin² x

sin² x cos² x

-dx +

sm xcos x

* MOf-*

’cos‘x ^Jsm*x

W powyższych całkach wykorzystano własności całki, wzory (1.1 HI .10) oraz wzory:

Wzór skróconego mnożenia: (a + b)² = a~ + lab + b² Definicje potęgi o wykładniku całkowitym i wymiernym:

1

+10    ;-~r~d-^x + <- =10f- ^ +10 f—-r— = 10/gx-10c/gx + C

^JSinⁱXCOS X    Jcns²y Jcin²v

(1.17)

x =

(1.18)

Wzory try gonometryczne:

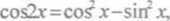
ctgx = —

cos x

sin x

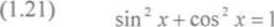
Uwaga:

Najczęściej pojawiającym się błędem przy stosowaniu wzoru (1.1) jest pomniejszanie wykładnika potęgi o wykładniku ujemnym oraz stosowanie wzoru (1.1) dla n = -1.

2.Calkowanie przez podstawianie

Całkowanie przez podstawianie polega na wprowadzeniu nowej zmiennej. Po wprowadzeniu nowej zmiennej wykonuje się także przekształcenie różniczki dx. W praktyce oznacza to, że oznaczając: G(x) = Tfu) otrzymujemy G ’(x)dx = T ’(u)Ju, skąd po dal--szych przekształceniach otrzymujemy dx. Sposób ten jasno pokażą przykłady.

W bardziej skomplikowanych przypadkach całkowania metodę tę stosujemy pośrednio przy okazji stosowania innej metody.

PRZYKŁADY CAŁKOWANIA

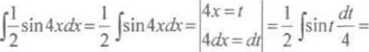
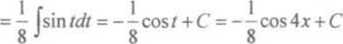
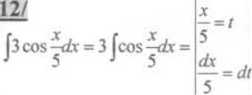
= 3 jScostó/ = 15 Jcos/<* =

= -I5sinf + C = -15sin —+C 5

-7-