19510 str014 (5)

14 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ
Rugując parametr t z układu (1), mamy
Jest to równanie prostej.
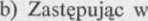
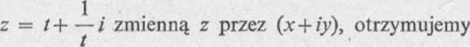
x + iy = t + — .
Porównując części rzeczywiste i urojone po obu stronach ostatniej równości, mamy
1
Rugując parametr / z układu (2), mamy
Jest to równanie hiperboli równobocznej.
Zadanie 2.2. Obliczyć pochodną funkcji: a) z = (1 + i)+(l +2i)f“, b) z = (l + 2/!)e2t.
Rozwiązanie, a)Zgodnie z uwagą 1 bieżącego paragrafu różniczkujemy naszą funkcję względem t, pamiętając, że i jest stałe. Mamy wtedy
J
z' = 2(l+2i)t.
b) Postępując analogicznie mamy
z' = 2iez,+ 2(l +2i!) e2t, z' = e2'(2i + 2+4if).
Zadanie 2.3. Obliczyć całki:
2
2
a) f (f + it2) dt, b) J (cos 21 +1 sin 2f) dl.
o
i
Rozwiązanie a) Przyjmijmy
(1)
z(0 = t + it2.
t i
Funkcja pierwotna G(t) funkcji (1) określona jest wzorem G(t) = — + —ł3. Wobec tego, zgodnie ze wzorem (2.5), mamy w naszym przypadku
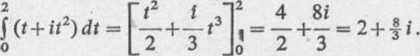
Wyszukiwarka
Podobne podstrony:
36778 str054 (5) 54 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zadanie 8.2. Obliczyć całkę0) gdz
str008 (5) 8 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Z wyrazów ciągu (1.4) tworzymy nowy ciąg
str024 (5) 24 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Stąd po przekształceniach dla a 0 mamy(
str042 (5) 42 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Wyznaczyć składowe Kx i Ky wektora natę
str050 (5) 50 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zauważmy teraz, że na O A = Jt mamy z =
20159 str096 (5) 96 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ 96 1. ELEMENTY TEORII FUNKCJI ZMI
75799 str120 (5) 120 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ dwóch cięć (rys. 1.44), homograf
79652 str018 (5) 18 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zadanie 2.7. Przez powierzchnię p
83008 str052 (5) 52 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ 88 52 1. ELEMENTY TEORII FUN
str012 (5) 12 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Funkcja zespolona zmiennej rzeczywistej
więcej podobnych podstron