16789 str100 (5)

100 !. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

100 !. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

(6)

w

bo wektor OB_l tworzy z dodatnim kierunkiem osi rzeczywistej O u kąt q> = — oraz

(3)    W-ł,

bo

IOBJ | B_łC,l    10,01    1

|/4B|    |BC,    |C4|    2 ’

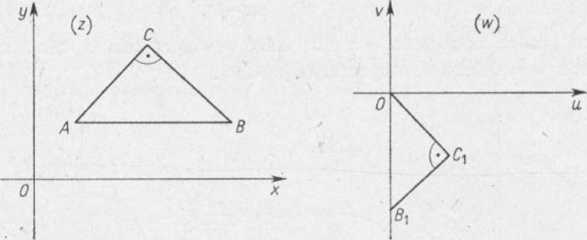
Rys. 1.25 Ale

(4)    n = |a|e'^Arga. Podstawiając związki (2) i (3) do wzoru (4), mamy

(5)    a = ie-ł^,K= -ł/#0. Przekształceniu (1) możemy teraz nadać postać

-H)-

Wierzchołek = (3+2/) ma przejść w wierzchołek iv_t = 0, wobec tego

'b¹

(7)    — *= —(3+21).

a

Podstawiając wzory (5) i (7) do wzoru (6), mamy

(8)    w= -iiz+Ofi-1).

/Wzór (8) jest rozwiązaniem naszego zadania.

Zadanie 11.5. Znaleźć przekształcenie homograficznc odwzorowujące okrąg |z| = 1 na oś rzeczywistą, aby punktom 1, i, —1 okręgu odpowiadały punkty —1, 0, 1 na osi.

Rozwiązanie. Zgodnie z twierdzeniem 7 szukane przekształcenie określone jest wzorem (11.6). Przyjmując w tym wzorze w, = — 1, w₂ = 0, tv₃ = 1 oraz z_t = 1, z₂ = i, z₃ = —1, otrzymujemy

w+l 1 + 1 _ z-1 -1-1 w—0 1—0 z —i —1—/

lub

(1)

Rozwiązując równanie (1) wz (2)

Wzór (2) określa szukane pr;

Zadanie 11.6. Znaleźć prz na oś rzeczywistą, aby punkt/ Rozwiązanie. Zgodnie z przekształcenie określone jest

gdzie

(2)    Wj = 0, w₃

Uwzględniając równości (2) v

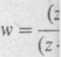
Wzór (3) określa szukane pr.

Zadanie 11.7. Znaleźć fun stkowe w siebie i taką, aby (1)

Rozwiązanie. Wiadomo foremnie koło jednostkowe w w punkt w = 0, jest homogr

(2)

gdzie cp oznacza dowolną lic: W rozważanym przypadł