27 (2)

Biblioteczka Opracowań Matematycznych

174/

jV* ln|x|c6r =

dx

" ^{= ,n}H ^du=— i

dv =

dx

x x

+ C

175/

}(4 + 3x)² lnj.r \Lx =

duM

u = ln|x|

A

</v = (4 + 3x)² v= J(l6 + 24x + 9x²)it = 16x + 12x = In|x|(l6x + 12.t² + 3x³)- J(l6 + 12x + 3x²)/x = (3x³ + 12x² + 16x)ln|x|-

+ 3x³

16x-6x² -x³ +C

176/

J.r ’ ln(x² + 3}/r =

2 xdx

u = ln(x² + 3) </«=-= ^v ' x +3 x⁴

dv = x'dx

v = -

₌ £l_lnM₊3|-ifi^L₌

4    ¹ I 2^Jx*+3

2\    S+3)    4 "    ^; 8    4    2^Jx²+3    4 '    ’

= x—----h^rdx = x—---

In 3 In3^J    !n3 In3 1n3

177/

Jx3'<Zx =

178/

m = x du = dx dv = y dx v = —

f X²£ĆC

x -3 = r

x = >//² + 3

, tdt tdt dx = — =

V/² +3

= — ln|x + -\/x' -3 + —xjx² -3 +C 2 I    2

179/ r	- f ^A
•*x^4+3x	^Jx^2(x^:+3)
I 4	5 Cx+D x
"ST* IJ + U) 1 H 1 H	x^2 x^2 +3
4 + C = 0	4 = 0
B+D = 0	fl = -3
3.4 = 0	c=o £> = -i
II <53

= /

Wracając do całki:

^-^|n[x² +3|-

-+— --ln^+sJ+C

8    4    4

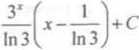
T3l+-/Vr²+3+C =

I 2

1 rdx I r    1 \/3    X

/ = - ——-=----arclg—j=+C

3^Jx² 3^Jx^s+3    3x    9    %/3

180/

1 r c/v

r ć/v r    <ix    V2 r t/f V2 r tńr I r

x²+l

jx^J    -2 J(*; ₊ lXx-y2 t + V2)⁼ T    2 Jx + >/2 2'

Powyższe współczynniki otrzymano z rozkładu podcałkowej funkcji wymiernej. A zatem:

f^₄_^_₂^=:yln|x-V2|-^ln|x + V2|-^arc/gx-t-C

181/

=    f-7^- f*. f^- = i_n|_/|-in|r ₊ i| ₊ c

^J/²(l+/) ^Jr(l + r)    ^J* + l

2x +1 = t 2dx = 2 tdt

C

^J(2x + lXl + V2.t + l)‘

= ln|V2x + l|-ln|lW2x+l| + C

182/

cos xdx

dx

r cos x    _ r cos xax _ r___ r ax

■’cos3x    ■* cos x(cos² x - 3 sin² x) ■* 1-sin² x-3sin²x ■U-4sin^:

= f—⁼ /

^J1 -3/²

tgx = t

i+r²

t²

d>_

_ j 1+/² _

i+/^!

4

1-3/²    1 —v/3r \ + &.i

aJJ-bJ3 = 0

.4 + fi = l

1+/²

fi t(.4>fi-Bj3)+A+B

1 — 3/

. = i 2

B = — 2

/ = - f ^d'_r -fi f ^dtr-- =--U= Inll - V3/| + —7=ln|l + V3/| + C =

2^J1-V3/ 2 •* 1 + y/3t 2^3 '    ¹ 2^3 ^1    1

l + V3/gx

2yf3

In

+ C

-53-