37

70

I

Podobnie jak we wzorze (3.21), jeżeli zastąpimy indeksy 1,.2 indeksami i, j, można wówczas rozpatrywać współczynniki wagowe (wagi) poszczególnych punktów wspólnych tak zwanej figury błędów, a błąd średni pozycji (radialny) M obliczyć ze wzoru:

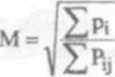
(4.3)

gdzie:

Pi - wagi poszczególnych alp.

P₁₍ - wagi poszczególnych punktów wspólnych par alp.

Ilustracją objaśniającą sposób wykorzystania współczynników wagowych jest wyznaczenie pozycji (estymacja) sposobem graficznym z trzech alp. Wykreśla się alp i w figurze błędów - trójkącie oblicza się dla każdego wierzchołka różnicę azymutów AAy (iys.4.1).    ^v

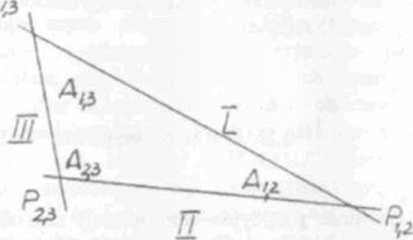
Rys 4 1 Trójkąt błędu trzech alp. u wierzchołków oznaczone są różnice azymutów AA^ poszczególnych punktów wspólnych

P

Wagi poszczególnych punktów' wspólnych oblicza się ze wzoru (3.21) zapisanego ogólnie:

Pi_j = p_ip_jsin²AA_jj

A

Na najdłuższym boku znajdujemy punkt podziału D, obliczany według określonych współczynników wagowych w odległości d od punktu o większej wadze (na rys. 4.2 punkt wierzchołka o większej wadze Pjj):

(4.4)

4-Pp

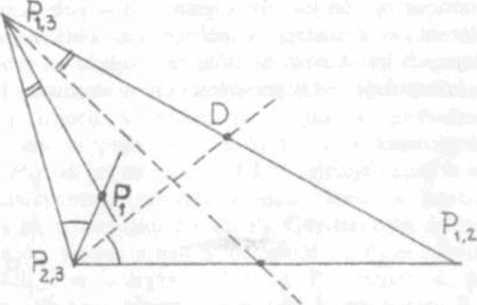
Rys 4.2 Graficzny sposób wyznaczima pozycji prawdopodobnej w trójkącie przecinających się alp

Punkt podziału odmierzamy od wierzchołka o współczynniku P|^ (większym niż Pj^) w skali zastosowanej do boku I. Z przeciwległego wierzchołka trójkąta (2,3) prowadzimy prostą do punktu D. Podobną procedurę stosujemy dla boku II, prowadząc z wierzchołka (1,3) prostą na kolejny punkt podziału boku 0. Proste, przeprowadzone do punktów podziału, mają punkt wspólny w środku trójkąta, wyznaczający pozycję prawdopodobną o błędzie średnim obliczanym ze wzoru (4.3).

Inny graficzny sposób wyznaczania punktu prawdopodobnego Pj przedstawiono na rysunku 4.2. Z wierzchołka trójkąta utworzonego przez trzy przecinające się linie pozycyjne, przeprowadzono środkową boku na przeciwległy (najdłuższy) bok trójkąta. Zmierzooo mniejszy kąt wewnętrzny między środkową a