38751 Untitled Scanned 91 (2)

6. RACHUNEK PRAWDOPODOBIEŃSTWA

CZĘSC TEORETYCZNA

KOMBINATORYKA

Reguła mnożeniu. Jeżeli pewnego wyboru IV dokonujemy w dwóch etapach i w pierwszym etapie możemy dokonać wyboru na i sposobów, a w drugim etapie na m sposobów, to wyboru W możemy dokonać na km sposobów.

Regułę mnożenia stosować można także wtedy, gdy wybom IV dokonujemy więcej niż w dwóch etapach. Np. jeżeli pewne-

gn wyboru IV dokonujemy w trzech etapach i w pierwszym etapie możemy dokonać wybom na k sposobów, w drugim etapie na m sposobów, a w trzecim na n sposobów, to wybom W możemy dokonać na kmn sposobów.

* Silnia:;i!= I-2-...-U, gdy /te N,. natomiast 0! = 1.

gdzie k. n -z N i k<n.

Liczba it-wy razowych wariacji z powtórzeniami //-elementowego zbiom A (czyli liczba k-wyrazowych ciągów o wyrazach

należących <fa zbioru A) jest równa //. (ozn. )

Liczba k-wyrazowych wariacji bez powtórzeń //'elementowego zbioru -A (czyli liczba k-wyrazowych ciągów o różnych

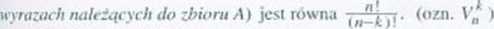
'■ Liczba permutacji //-elementowego zbioru A {czyli liczba n-wy razowych ciągów o różnych wyrazach należących zbioru .dl jest równan!. (ozn. P_n)

«• Liczba /•elementowych kombinacji //-elementowego zbioru A (czyli liczba k-clcmcniowych podzbiorórw zbioru /A) jest

równa

KLASYCZNA DEFINICJA PRAWDOPODOBIEŃSTWA

«> Jeżeli wszystkie zdarzenia elementarne należące do zbioru ii są jednakowo prawdopodobne, to prawdopodobieństwo

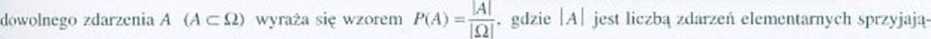
cych zdarzeniu .A. a i iż! jest liczbą wszystkich zdarzeń elementarnych.

NIEKTÓRE WŁASNOŚCI PRAWDOPODOBIEŃSTWA

Jeśli ii jest zbiorem zdarzeń elementarnych, a /’ prawdopodobieństwem określonym na zdarzeniach zawartych w zbiorze ii. lii dla dowolnych zdarzeń A, li a ii

*    misi.

*    r(A) t r(A^r) - I. gilzie .-A' jest zdarzeniem przeciwnym do zdarzenia .A.

*    m u B)=P(A) + /'(li) - P( A r> li».

ZADANIA WPROWADZAJĄCE

Zdający potrafi • obliczać unitowi n! i

6.1 Oblicz a) 4!:    b) jj;

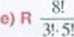
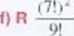
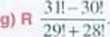
6.2 R Sprowadź do prostszej postaci wyrażenie a)    b)    c) (2/r)! + (2/i    l)! + (2n-2)!.