41530 str092 (5)

92 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

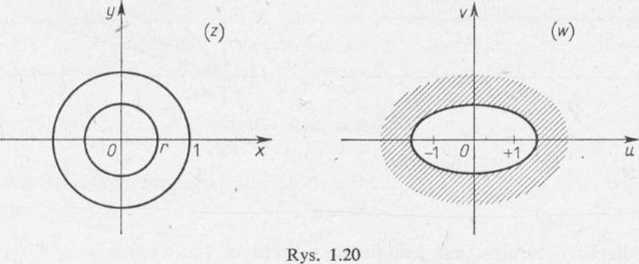
Jeżeli w (11.9) zastąpić z przez 1/z, to prawa strona nie ulegnie zmianie, a wnętrze koła |z|<l przejdzie w jego zewnętrze. Stąd wniosek: Funkcja (11.9) odwzorowuje konforemnie zewnętrze koła |z|>r o promieniu r>l na zewnętrze elipsy (11.9'), a zewnętrze koła |z|>l na całą płaszczyznę rozciętą wzdłuż odcinka — 1<m<1.

92 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Z równań (11.10') wynika < — ^ji<x<iit osi rzeczywistej u w odcinek — 1 <u< 1 osi rzecz) przechodzi na płaszczyźnie zm

4" Funkcja

(11.10)

w = sin z

(11.10"') , 1

Oczywiście hiperbole (11.10") i x= const i y = const do siebl wuje konforemnie pionowy pa nej (w) rozciętą wzdłuż dwócl

Uwaga. Analogicznie, na wzorowuje każdy pas pionow;

(2k-l)|it<

Twierdzenie 8. Długość Lc waniu konforemnym w = f(z)

jest jednolistna w nieskończonym pasie pionowym —^7t<Rez<^rc. Przyjmując w — u + iv, z = x + iy i stosując wzory Eulera, otrzymujemy po rozdzieleniu części rzeczywistej i urojonej

e>' + e~^y    e^y-e~^y

(11.10')    u ————sinx,    v — —-—cos*.

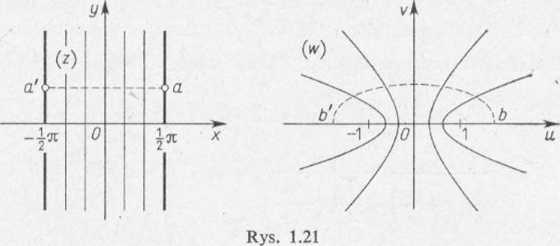
Z (11.10') wynika, że oś urojona Oy odwzorowuje się w oś urojoną Ov (rys. 1.21), bo gdy x — 0, wówczas u = 0. Natomiast każda prosta x = const # 0, równoległa do osi urojonej Oy przechodzi przy odwzorowaniu (11.10) na płaszczyźnie zmiennej (w) w jedną gałąź hiperboli o równaniu

(11.11)

Twierdzenie 9. Pole S ob wyraża się wzorem'.

(11.12)

B. Funkcja Greena i jej zwiąa

Definicja 8. Niech D bę spójnym lub wielospójnym), < wolny punkt obszaru D (nie w; wista G{z) = G(x,y) dwóch z funkcją Greena dla obszaru D warunki:

1° jest harmoniczna i dod 2° dąży do zera, gdy pun 3° różnice

(11.13)    G(

(11.13')    ¹

(11.10")

sin² x cos² x

= 1.

dążą do granicy skończonej, znaczenia, że punkt z₀ jest 1

Równanie (11.10") otrzymujemy rugując zmienną y ze związków (11.10').