58893 Image0030

12G Szkoła - segregacje - nierówności

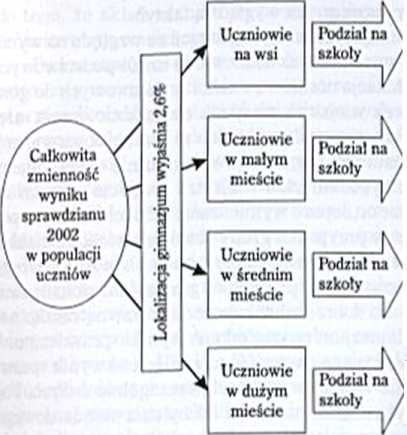
Czynnik lokalizacji szkoły wyjaśnia tylko trochę ponad 2% zmienności wyników sprawdzianu. Znacznie więcej wyjaśnia podział na szkoły. Jak widzimy, w roku 2002 najbardziej zróżnicowane są szkoły podstawowe zlokalizowane w dużych miastach, następnie grupa szkól wiejskich. Szkoły podstawowe zlokalizowane w małych i średnich miastach to segment systemu zdecydowanie słabiej zróżnicowany. W sumie możemy powiedzieć, że zróżnicowanie szkół ze względu na wyniki kształcenia jest znaczące, ale niezbyt silne. Wyniki są oczywiście bardzo zbliżone do prezentowanych w rozdziale 1, choć zgodnie z tym, co zostało powiedziane wyżej, ze względu na niclosowc braki danych oszacowania te są trochę niższe niż dla pełnej populacji.

Przechodzimy do drugiego, najważniejszego etapu naszej analizy. Ze szkól jiod-stawowych interesująca nas kohorta uczniów we wrześniu 2002 roku trafiła do gimnazjów. W jakim stopniu wynik sprawdzianu wiąże się z lokalizacją gimnazjum, jak silna jest segregacja międzyszkolna oraz jakie jest natężenie segregacji wewnątrzszkolncj ze względu na uprzednie osiągnięcia? Statystyczna metoda szacowania segregacji jest analogiczna do badania zróżnicowania szkół ze względu na wyniki kształcenia. Sprawę komplikuje - |>odol)nic jak w metodzie szacowania efektów segregacji ze względu na SES rodziny ucznia (poprzedni jiodrozdzial) - wprowadzenie trzeciego poziomu analizy - klas szkolnych. Procedura wygląda następująco. Najpierw analizowane jest zróżnicowanie związane z jiodziałem ze względu na lokalizację gimnazjum. Następnie uczniów w każdym segmencie gimnazjów* wyróżnionych ze względu na czynnik wielkości miejscowości traktuje się jako jedną grupę badanych i oblicza się stosunek wariancji międzyszkolnej do wariancji całkowitej w danq grupie. W ostatnim kroku wykonuje się analogiczną analizę z tą różnicą, że oblicza się stosunek wariancji międzyoddzialowcj (dla wszystkich oddziałów klasowych w danej grupie placówek) do wariancji całkowitej wyników uczniów w danym segmencie gimnazjów. Jeżeli od procentu wariancji wyników* sprawdzianu wyjaśnianego przez i>odzia! uczniów* na oddziały odejmiemy wskaźnik segregacji międzyszkolnej, to otrzymujemy oszacowanie średniego wskaźnika segregacji wewnątrzszkolnej. Właściwsze byłoby bardziej złożone szacowanie nasilenia tej segregacji, polegające na obliczeniu oddzielnie dla każdego gimnazjum w*skaźnika segregacji w*ewnątrzszkolnej (stosunek wariancji międzygrupowej związanej z podziałem uczniów na oddziały klasow*e do wariancji całkowitej wyników sprawdzianu w danym gimnazjum; z definicji w gimnazjum jednooddzialowym w-skaźnik ten przybiera w*artość 0%), a następnie obliczenie dla danej grupy gimnazjów średniej w*ażoncj tych wskaźników. Jednak okazuje się, że ta metoda daje praktycznie identyczne oszacowanie nasilenia segregacji wewnątrzszkolncj dla danej grupy szkól w jiorównaniu z szacowaniem uproszczonym.

Szacunek segregacji międzyszkolnych, a szczególnie wewnątrzszkolnych na progu gimnazjów, obarczony jest błędem sj>owodowanym tym, że w bazie danych egzaminacyjnych mamy informację o tym, do której szkoły i klasy uczęszczał uczeń, gdy kończył, a nie rozj>oczynal naukę w szkole. Wielkość tego błędu trudno oszacować, brak bowiem informacji o migracji międzyszkolnej w trakcie nauki w gimnazjum oraz o skali zjawiska iłolegającego na zmianie klasy w trakcie nauki w* danym gimnazjum. Można mieć nadzieję, że w wypadku segregacji międzyszkolnej błąd ten jest minimalny, jednak w wypadku segregacji wew*nątrzszkolnych można przypuszczać, że jioziom tej segregacji na progu gimnazjum jest niższy niż na końcu trzyletniego okresu nauki.

Rozdział 2. Poziom segregacji społecznych w polskiej oświacie

127

Wyniki analizy procesów segregacji w gimnazjach dla kohorty 2002=^2005 przedstawia poniższy schemat.

Wyjaśnia 6,1% zmienności	!\xlziat na klasy
	~v
Wyjaśnia 6,1% zmienności	hidzial na klasy
	“V
Wyjaśnia 6,9% zmienności	!\xlzia! na klasy

Wyjaśnia średnio 4,3% zmienności

Wyjaśnia średnio 9,5% zmienności

Wyjaśnia średnio 11,2% zmienności

Wyjaśnia 14,3%	Podział na
zmienności	klasy

Wyjaśnia średnio 10% zmienności

Schemat 2.4. Efekt segregacji na poziomie gimnazjalnym w 2002 roku obliczony na podstawie wyniku sprawdzianu po szkole podstawowej ze względu na lokalizację gimnazjum, chodzenie ucznia do danego gimnazjum oraz dodanej klasy w gimnazjum

Obliczenia własne na f>odslau ie danych CKE

Przy|K>mnijmy, że najpierw oszacowano, jaki procent zmienności wyniku sprawdzianu wyjaśnia czynnik lokalizacji gimnazjum. To oszacowanie nic powinno znacząco odbiegać od wyniku dla szkól jtodstawowych. Ewentualna różnica wskazywałaby na uczniowskie migracje „między" kategoriami lokalizacji szkoły. Gdyby, na przykład, lepsi absolwenci wiejskich szkól podstawowych w dużej liczbie przechodzili do miejskich gimnazjów, to można by oczekiwać, że czynnik lokalizacji gimnazjum wyjaśniałby większy odsetek wariancji wyników sprawdzianu niż lokalizacja szkoły j>odstawowcj.

Analiza danych zgromadzonych w bazach egzaminacyjnych pozwala oszacować poziom migracji. Okazuje się, że około 15% uczniów kontynuowało naukę w gimnazjum zlokalizowanym w miejscowości o innej „przynależności" do kategorii urbanizacyjnej w stosunku do szkoły podstawowej. W przypadku absolwentów wiejskich szkól podstawowych około 17% uczniów kontynuowało naukę w gimnazjum miejskim, w tym 1% w wielkomiejskim.

Wyniki przedstawione na powyższym schemacie pokazują, że lokalizacja gimnazjum wyjaśnia tylko o 0,4 punkty procentowe więcej zmienności wyniku sprawdzianu niż w przypadku szkól podstawowych. To minimalna różnica, więc migracja uczniów wiejskich |x> ukończeniu szkoły jtodstawowej do pobliskich miejskich gimnazjów prawdopodobnie słabo wiąże się z poziomem osiągnięć uczniów.

Popatrzmy na segregację międzyszkolną. Jednym z celów wprowadzenia gimnazjów w ramach reformy Handkcgo miało być stworzenie segmentu szkól mniej we-