68900 SPOM02

• Zadanie >1: Estymaty /), i p₂ parametrów /;, i p₂ inode;u obiektu pomiaru: y -    + p_}x_:,

wyznaczono przy użyciu planu eksperymentu:

fi o il^r

X =

°    1 l_v

na podstawie danych obarczonych błędem przypadkowym o rozkładzie normalnym z zerową wartością oczekiwaną i wariancją a² =10"'. Oszacować wariancję odpowiedzi tego modelu na wymuszenie .r, = ,r₂ = 1.

L>t

W

l/'⁷

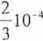
Rozwiązanie:

XX =

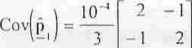
2 -1 -1 2

Var

Var

	„ - \^2~		- V^2'
feM	\PX> ^+ £2^Xi]	= E	l£, ^+£j
	., i r„ .f		I0~* r
(i)-^E	?;J^+2E[e,^]	+E[	&]•—t^2

Zadanie 5: Estymaty /), i p₂ parametrów p_{ i p₂ następującego modelu toru pomiarowego: z = J\ + p_ix_l + p,x,

(gdzie r - surowy wynik pomiaru, x_{ - meznrand, x₂ - wielkość wpływająca) wyznaczono metodą najmniejszych kwadratów, dokonując następującej transformacji danych pomiarowych, reprezentujących surowy wynik pomiaru: y„ = z² -1 dla/j = l...../V

Oszacować błąd systematyczny (obciążenie) tych estymat, spowodowany odstępstwem od założeń klasycznej metody najmniejszych kwadratów. Do obliczeń przyjąć:

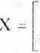
oraz założenie, że = z„ -    , gdzie Az_n są realizacjami niezależnych zmiennych losowych o

zerowej wartości oczekiwanej i wariancji g:

Ro/w inznnic:

XX

0    ^;    2,0 1 j

Af> - E[p)-p-(X^TX)Ś*g|y >]-(x^r\)X^Tli[Ay