224 (19)

oraz

Ra • 0 + R_b ■ Ib ~    = 0    (14.8)

Równania 14.7 i 14.8 wyrażają warunki równowagi statycznej. Rozwiązując te dwa równania można określić wielkość sił reakcji podpór R_A i R_B:

Rb

P ■ l

(2 ' l_B)

10 • 10 2 • 8

= 6,25 N

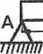
. P ■ (2 • l_B - O

Ponieważ ciężar belki rozłożony jest równomiernie wzdłuż całej belki, a siły reakcji podpór skupione są w dwóch miejscach A i B, przeto w belce wystąpią naprężenia wywołujące odkształcenia, którym przeciwstawiają się siły spójności materiału. Występujące naprężenia będą usiłowały wygiąć belkę (moment gnący) oraz przesunąć względem siebie warstwy materiału (siły tnące). W celu określenia wielkości tych sił przyjęto następującą regułę znaków:

—    siły ciężkości przyjmują znak ujemny,

—    moment gnący działający w kierunku wygięcia belki w dół przyjmuje znak dodatni (rys. 142).

W celu określenia wielkości sił tnących (ST), w dowolnym przekroju belki dzielimy ją umownie na część prawą i lewą w stosunku do badanego przekroju.

Siła tnąca w danym przekroju poprzecznym jest to algebraiczna suma wszystkich sił zewnętrznych leżących po jednej stronie danego przekroju i prostopadłych do osi wzdłużnej belki.

_ 10 (2 8- 10) _ „₅ N

2-8

i ii i^P i i i T~n

⁸ vmri?

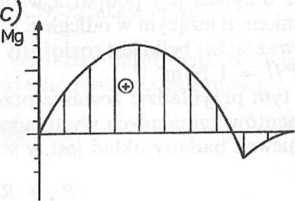
Rys. 141. Siły tnące (b) i momenty gnące (c) występujące w belce (a)

madę by voyteck (dec * 2004)

224