246 (11)

9. R o c k u n • li p r o w d o p o d o b i e ń * t w o

9.3.3. Obliczanie prawdopodobieństwa sumy zdarzeń

9. R o c k u n • li p r o w d o p o d o b i e ń * t w o

Analizując treści zadań, w niektórych z nich odnajdujemy spójnik „lub", któremu w probabilistyce odpowiada suma zdarzeń: A U B (por. w 9.2.2c.). I\> właściwym zdefiniowaniu każdego ze zdarzeń: A, B. należy sięgnąć po wzór na prawdopodobieństwo sumy zdarzeń: A i B.

Dysponuje my dwoma wzorami na prawdopodobieństwo sumy zdarzeń (por. uwaga w 9.2.3c.), stąd też należy' ustalić możliwość zajścia iloczynu ustalonych zdarzeń: A n B. Jeśli iloczyn ten jest zdarzeniem niemożliwym, to korzystamy z aksjomatu (A2) (por. 9.2.3b.). Gdy zaś A n B jest możliwy, to stosujemy własność (c4) (por. 9.2.3c.). Oto przykłady: a) Oblicz prawdopodobieństwo tego, że losując 5 kul spośród 4 kul białych i 6 czarnych, otrzymamy co najwyżej 2 kule czarne.

Na początek określamy przestrzeń ii. ii — losowanie 5 kul spośród 10 (4 białe -+- 6 czarnych) bez ważnej kolejności

= |a>= |x_|,.t,.A:j..v₄..v_s}:x.e {zbiór 10 kul:

4 białe -4- 6 czarnych} Ai € {l, 2, 3, 4. 5}|

S=<=(^,5°)

Należy obliczyć prawdopodobieństwo tego, że wylosujemy: co nąjwyżej 2 kule czarne, czyli: dokładnie 2 kule czarne: A lub dokładnie jedną kulę czarną: B (zdarzenie: zero kul czarnych to jest zdarzenie: 5 kul białych nie jest ono możliwe, bo losujemy 5 kul, a białych jest tylko 4 wśród 10). Zdarzenia A i B są wykluczające (niemożliwe jest bowiem, aby wylosować równocześnie dokładnie 2 kule czarne i dokładnie 1 kulę czarną). Stosujemy więc wzór na prawdopodobieństwo sumy zdarzeń wykluczających się: P( A U B) =P( A) -+- P(B). 'Wystarczy

zatem z klasycznej definicji prawdopodobieństwa obliczyć BA oraz PB i podstawić do powyższego wzoru:

(z 6 czarnych losujemy 2 kule czarne)

(z 4 białych losujemy 3 kule białe)

(razem jest 5 wylosowanych kul: 2 czarne i 3 białe)

B =

II18

(z 6 czarnych losujemy jedną kulę)

(z 4 białych losujemy 4 kule białe)

(razer

■ jest S wylosowanych kul: I czarna i 4 białe)

P( A U B)= P(A)+ P(B) =

Wam is®

li li

to jest poszukiwane prawdopodobieństwo b) Oblicz prawdopodobieństwo tego, że przypadkowo wylosowana liczba naturalna jest podziel-na przez 2 lub 3.

Otóż spójnik „lub” znajduje się między następująco zdefiniowanymi zdarzeniami A i B: A — przypadkowo wylosowana liczba naturalna jest po-dzielna przez 2, B — przypadkowo wylosowana liczba naturalna jest podzielna przez 3. Zdarzenie A n B — oznacza, że przypadkowo wylosowana liczba naturalna jest podzielna przez 2 i przez 3 (iloczynowi odpowiada spójnik „i”), czyli jest podzielna przez 6. Korzystamy zatem ze wzoru na prawdopodobieństwo sumy. zdarzeń dowolnych (niewykluczających się):

P(Ai> B) = PA + PB - PAB = 4- + ł- i = T

(co druga liczba naturalna jest podzielna przez 2)

Zatem poszukiwane 2_

3'

(co trzecia liczba naturalna jest podzielna przez 3)

(co szósta liczba naturalna jest podzielna przez 6)

prawdopodobieństwo jest

równe

9.3.4. Obliczanie prawdopodobieństw zdarzeń za pomocą drzewa probabilistycznego (I)

Jeśli doświadczenie losowe jest wieloetapowe, a zdarzenia elementarne tworzą skomplikowany zbiór, wówczas pewnym ułatwieniem jest tzw. drzewo probabilistyczne, a) Pojęcie drzewa probabilistycznego

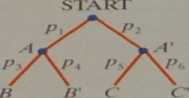
Jest to graf składający się z krawędzi i wierzchołków, ilustrujący przebieg wieloetapowego doświadczenia losowego. Krawędzie odpowiadają zdarzeniom losowym, a wierzchołki wynikom poszczególnych etapów. Przy poszczególnych krawędziach zapisuje się prawdopodobieństwa odpowiednich zdarzeń. Poziomy rząd krawędzi symbolizuje określony etap doświadczenia losowego. Suma prawdopodobieństw przypisanych krawędziom wychodzącym z jednego wierzchołka jest równa 1. Rysunek przedstawia drzewo probabilistyczna w ogólnym przypadku:

I    etap (p, -+- p_: = 1)

II    etap (p₃ -t- p₄ = 1 ;p_s + p_b - I)

Ciąg krawędzi od startu do ostatniego wierzchołka to gałąź drzewa. Aby obliczyć prawdopodobieństwo zdarzenia wieloetapowego reprezentowanego przez jedną gałąź, należy wynmożyć prawdopodobieństwa przypisane poszczególnym krawędziom tej gałęzi (tj. tzw. reguła iloczynów). Zdarzenie reprezentowane przez kilka gałęzi jest sumą zdarzeń opisanych przez gałęzie, a jego prawdopodobieństwo jest sumą prawdopodobieństw zdarzeń odpowiednich gałęzi (tj. tzw. reguła sum). Na przykład: P{ AB U A 'C ) - p_x p _x -ł- />, p