252 (19)

504 19. Zastosowanie przekształcenia dyskretnego %

Przykład 2. Wyznaczymy napięcia U_h (n = 0, 1, 2,...) w układzie drabinkowym przedstawiony^ rys. 19.2.

Na podstawie I prawa Kirchhofla dla węzła n + 1 mamy

U.-V'+1    U.+ ,-Un₊2 _n

R    R    R

n    R n+1 R n+2 R

€ZD—

£|Q r\\\uo *[][</,

* lu,

* I \U,

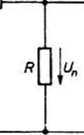
Rys. 19.2. Układ drabinkowy zasilony napięciem stałym

skąd otrzymuje się równanie różnicowe

l^n + 2^-31/,+ i + U, = 0.

Równanie prądowe dla węzła 0 przybiera postać

£    £ E-U.

~W' ⁺ H⁺ R ⁼ °’

gdzie R_e oznacza rezystancję wejściową omawianego układu, a stąd znajdujemy

Wykorzystując powyższy wzór oraz oczywistą zależność U₀ = £, qtrzymujemy na podstawie wyrażenia (19.14):

^{l/„₊₂} =z²(/(_Z)-£z²-^2-^£,

zU(z)-Ez,

przy czym V(z) = iż^- {{/„}. Po przekształceniu równania różnicowego opisującego badany układ znajdujemy

U(_Z) = (^z2~^gz)^£ ₌ U²-«z)E z² — 3z + f (z—z,)(z—z₂)’

gdzie a=l+R/R_e oraz z, = -(3 + ^/5), z₂ =-(3—^/5). Wyznaczając oryginał tej transformaty z*

pomocą metody omówionej w p. 19.4.2, otrzymujemy rozwiązanie rozpatrywanego równania różnicowego:

U, =-[(z,-a)z^-(z₂-a)z5], n = 0, 1,2N.

Przypuśćmy, że badany układ pracuje w stanie zwarcia, czyli U_s = 0. Wobec tego na podstawie _wzoru na U, otrzymujemy (z, — a)z* = (z₂ — x)z2, a stąd

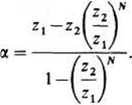
Podstawiając tę zależność do wzoru na U„, znajdujemy

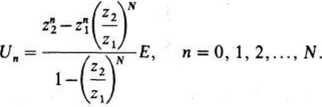
W przypadku układu nieskończonego należy przyjąć Noo. Biorąc pod uwagę, że z, > z₂, wobec tego dla N -*oo, otrzymujemy

U_m=Ez5,    u = 0,1,2.....

przy czym z₂ < 1.

19.6. Transmitancja dyskretna. Dyskretna odpowiedź impulsowa

19.6.1. Określenie transmitancji dyskretnej

Przypuśćmy, że do wejścia układu liniowego doprowadza się ciąg impulsów {x„}, będący dyskretnym wymuszeniem, próbkowanym za pomocą funkcji impulsowania (19.1). Odpowiedź omawianego układu jest w ogólnym przypadku funkcją ciągłą, a po jej dyskretyzacji za pomocą funkcji impulsowania (19.1) otrzymuje się dyskretną odpowiedź o postaci ciągu impulsów {y„}; jest to zatem odpowiedź układu dyskretnego.

Transmitancją dyskretną T{z) nazywamy iloraz transformat odpowiedzi dyskretnej i wymuszenia dyskretnego, przy zerowych warunkach początkowych:

(19.35)

T(z) =

_ Y(z)

&{x_n}    X(z)'

19.6.2. Dyskretna odpowiedź impulsowa

Dyskretną funkcję impulsową {£„} określa się w sposób następujący:

<5(n) = <5„

1,    gdy    n = 0,

0,    gdy    n # 0.

(19.36)

Wykres tej funkcji jest przedstawiony na rys. 19.3. Z określenia przekształcenia & wynika, że transformata dyskretnej funkcji impulsowej

(19.37)

•3T{<5(n)} =&{ó_n} = 1.