250 (18)

500

19. Zastosowanie przekształcenia dyskretnego 2t

a następnie dzieląc licznik przez mianownik, otrzymujemy:

+ 13z‘² + 40z~³ + ...

1    :(1 — 4z"‘+3z~²) = l+4z‘

1—4z~*+3z'²

4z~' —3z~² 4z-‘-16z-² + 12z-^ł

13z‘²-12z‘³ 13z~² —52z~³ + 39z~⁴

40z~³ —39z~⁴ 40z-³-160z-⁴+120z'⁵

wobec tego

F(z) = 1+4z-' + 13z-² + 40z-³+...

skąd

/o = 1. /i = 4, fi = 13, /j = 40,...

Metoda ta jest wygodna, gdy celem obliczeń jest kilka początkowych wyrazów ciągu {/„}•

19.4.2. Metoda rozkładu na ułamki proste

Zakładamy, że równanie charakterystyczne transformaty

^am^zm + ^am-₁z^m~¹ + ... + a₁z+a₀ = 0    (19.27)

ma różne od zera pierwiastki jednokrotne z_t, z₂,z_m. Jak wiadomo, funkcję wymierną (19.24) przy m > v można wyrazić wzorem

(19.28)

G(z) _ y A_k H(z) * = !Z-Z*’

gdzie A_k, k = 1, 2,..., m, są stałymi. Powyższe równanie mnożymy stronami przez z —Zj, i — 1,2,..., m, otrzymujemy

G(z)

H(z)

Z

k= 1 fc*i

(z Zj) = Ai + (z-Zj)

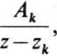
a po przejściu do granicy przy z->z_t

A: = lim

G(z)(z-z,) H(z) ‘

Stąd po zmianie i na k oraz zastosowaniu reguły de THospitala, znajdujemy

G(z)(z—z_k) G(z_t)

A_k = lim

Z — Zk

H(z)

H'(z_ky

(19.29)

501

19.4. Przekształcenie odwrotne

Wykorzystując zależność (19.11), można wyrażenie (19.28) przedstawić w postaci

A_kar{żl~^le(n-l)},

H\^Z) k= 1

_a zgodnie z określeniem przekształcenia    mamy 2t{Ą ^le(n — 1)} =

X

= V    (n—    wobec tego

n = 0

= Z ^ Z ** ¹e(n— 1)^ " = X ² "e(n-l) Z ^*1 *•

G(z)

^(^Z) k= 1 n = 0    n = 0    *=1

Wynika więc, że ogólny wyraz oryginału dyskretnego {/„} ma postać

/„ = £(«-1) I 4^ ¹-

* = 1

Ponieważ e(n — 1) = 1 dla n ^ 1 oraz e(n— 1) = 0 dla n = 0, otrzymujemy po wzięciu pod uwagę zależności (19.29) wzór przedstawiający ogólny wyraz oryginału {/„}:

(19.30)

r

f _ y G(z_k) ,

przy czym /₀ = 0.

Gdy wielomiany G(z) i H(z) w zależności (19.24) są tego samego stopnia (m = v), należy najpierw podzielić G(z) przez H(z), otrzymując w ten sposób /₀ = bja_m. Dowodzi się, że pozostałe wyrazy ciągu/, ,/₂,... można obliczać na podstawie wzoru

(19.30).

Przykład 2. Obliczymy oryginał transformaty z przykładu 1.

Mamy tu G(z) = z², //(z) = z² —4z + 3 i H'(z) = 2z—4, a pierwiastkami równania W(z) = 0 są z, = 1 i :₂ = 3. Ponieważ wielomiany G(z) i H(z) są tego samego stopnia, więc po podzieleniu G(z) przez H(z) znajdujemy f₀ = 1. Przyjmując m = 2 we wzorze (19.30), otrzymujemy a stąd /_t = 4, f₂ = 13, /₃ = 40,..., zgodnie z wynikiem otrzymanym w przykładzie 1.

Przypadku pierwiastków wielokrotnych nie będziemy rozpatrywać. Jest on omówiony w pracy [28],

19.5. Równania różnicowe

19.5.1. Uwagi ogólne

Przy rozwiązywaniu równań różniczkowych na emc dokonuje się dyskretyzacji, rozpatrując wartości funkcji w regularnych chwilach t_k, k = 0, 1, 2,..., o stałym